[ 알고리즘 ] 19. Floyd Algorithm
Floyd Algorithm
: All Pairs Shortest Path 를 구하기 위한 알고리즘이다.
From all to all

Dense graph는, Edge의 개수 = O(V^2)인 경우의 graph이다.
E에 V^2를 대입하면 과 같다
● Floyd Algorithm 사용 조건
- Negative Edge 는 가능
- 하지만 Negative Weight cycle은 안 된다.
- DP로 구현한다. = Optimal Substructure 적용 가능
알아야 하는 개념
- Intermediate Vertex
: i에서 k까지 가는 path에 포함되는 Vertex
단, 한 번만 나올 수 있다.
DP로 생각해보면 1 ~ ... k-1까지 가는 최단 경로를 찾았다면
k까지 갈 땐 k-1까지의 최단 경로를 사용하여 길을 찾을 수 있다.
shortest path에서는 같은 vertex가 2번 선택되지 않는다.
대략적인 푸는 개념
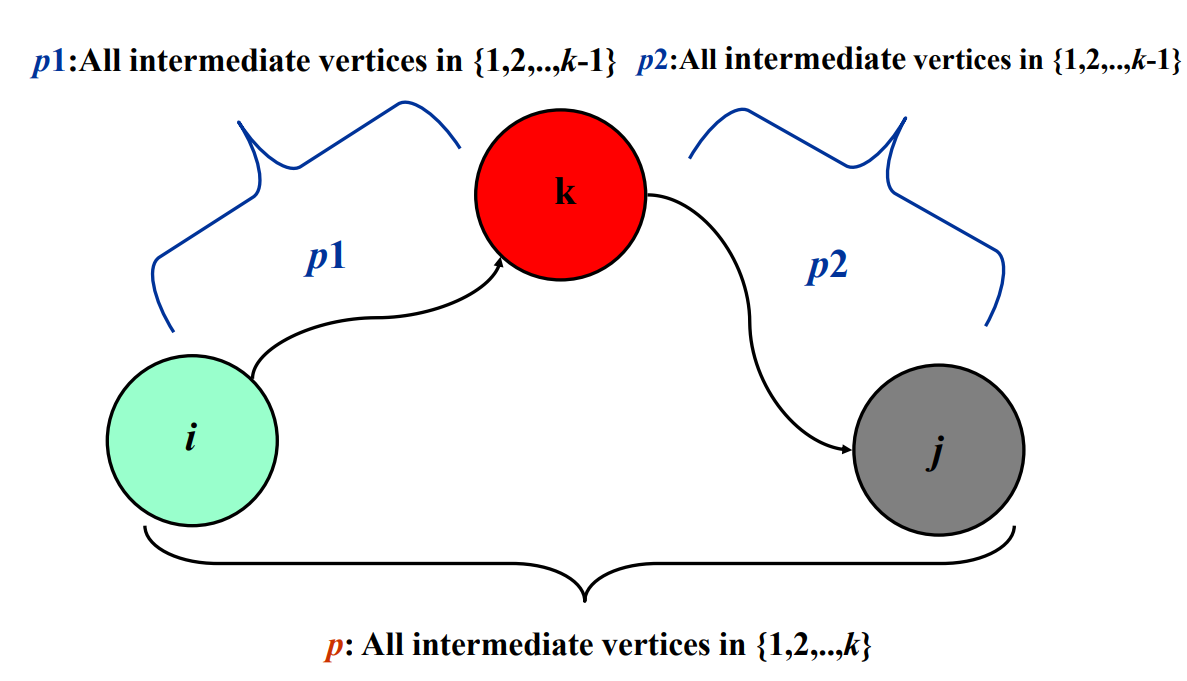
i에서 j까지 가는 최단 거리를 p라고 가정한다.
vertex들은 {1,...k-1}까지 가 intermediate가 될수 있다.
- Case 1 : k가 p의 intermediate가 아닐 때
= Shortest path 의 intermediate 는 { 1 ~ k-1 }이다.
- Case 2 : k가 p의 intermediate일 때
= Path p는 p1 = [ i ~ k ] / p2= [ k~ j ]로 나눌 수 있다.
p1 즉, i~k 사이에 올 수 있는 intermediate vertex는 {1~k-1}
p2 k~j 사이에도 올 수 있는 intermediate vertex는 {1~k-1}

d ij (k)
= i~j까지 가는 최단 경로에 Intermediate vertex는 {1~k}가 될 수 있다.
D(k)
= n*n matrix를 만든 것 [ d ij (k) ] ▼
- 세로 = 출발하는 node
- 가로 = 도착하는 node
- D(a) = intermediate vertex로 a를 추가(고려).
ex ) D(0) = 1에서 0을 거쳐서 가는 Distance
- ㅠ는 현재 새롭게 추가된 intermediate 로 인해서
경로가 새로 업데이트되는 경우에 해당 intermediate vertex를 업데이트 한다.
= D를 통해 Distance를 구하고
ㅠ 를 통해서 Path를 구한다.
d ij(0) 이면 그냥 각자의 weight으로 matrix를 채우면 된다
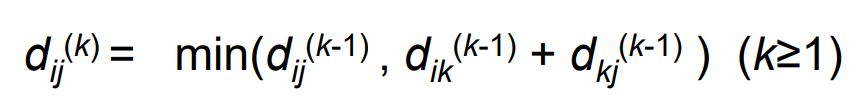
k가 Intermediate가 아닌 경우 vs 맞는 경우 중에서 작은 걸 골라 d ij (k)로 설정한다.
▼ 예
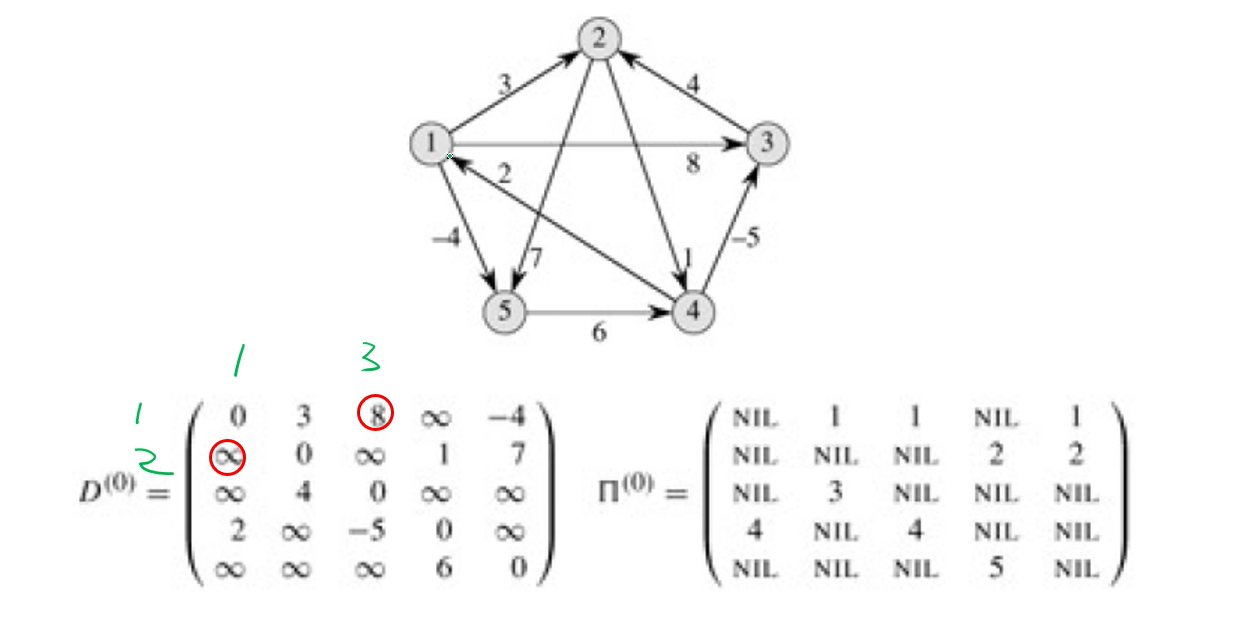
1번에서 3번으로 가는 edge = 8
2번에서 1번으로 가는 edge = 무한대
2번에서 3번 가는 edge = 무한대
4번에서 5번 가는 edge = 무한대
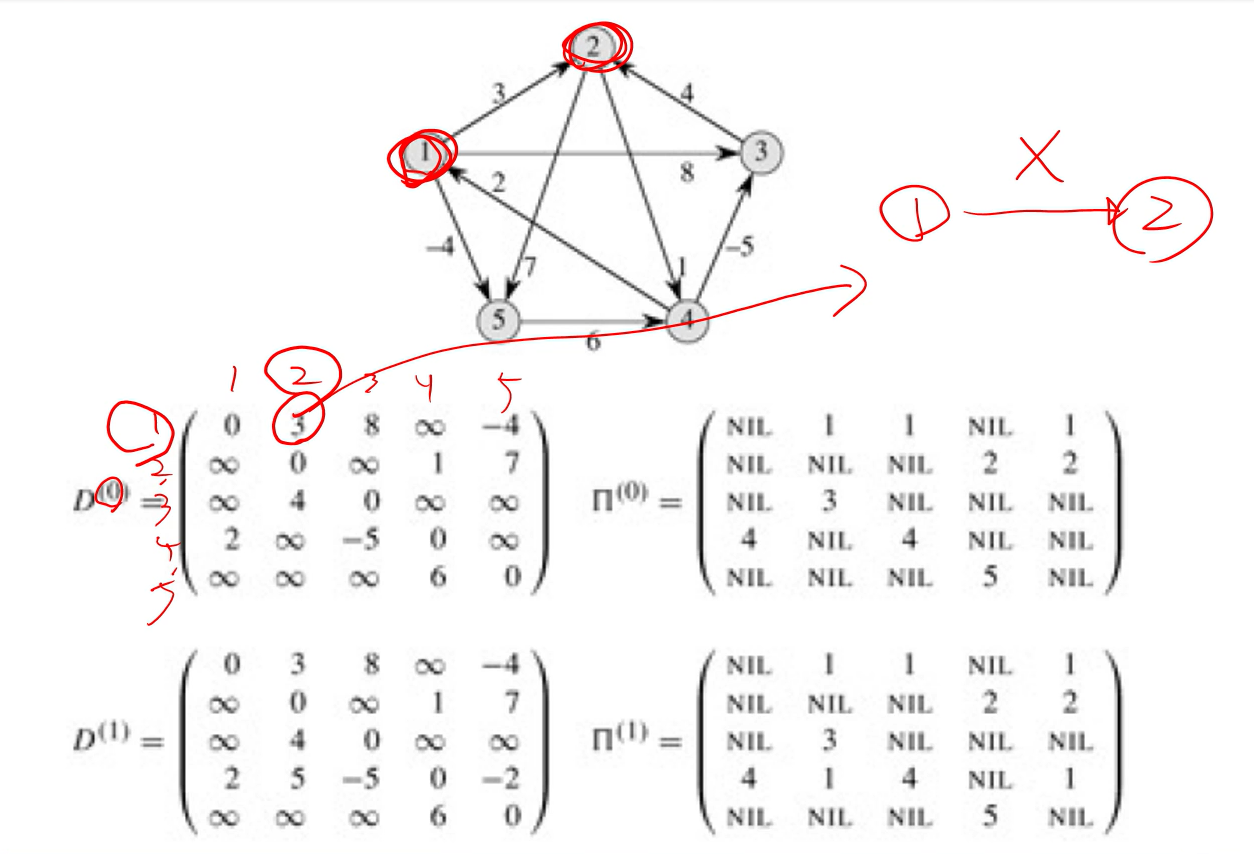
만약에 1번 vertex를 intermediate로 추가하면
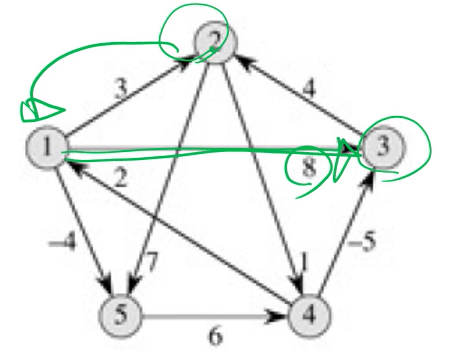
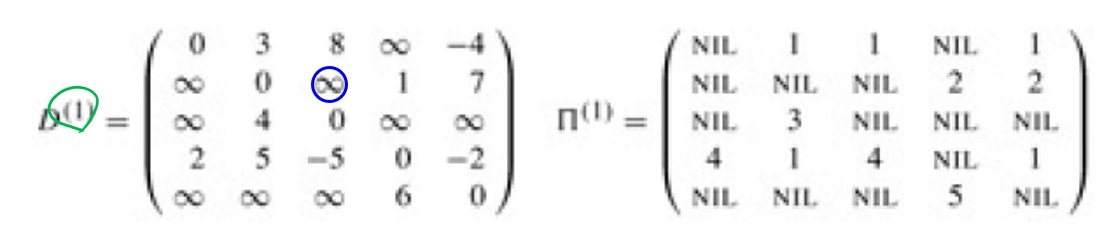
4 1 5가 가능하기 때문에 2 +(-4) 를 해서 -2를 추가할 수 있고,
ㅠ에는 1을 통해 minmum이 되었기에 1을 추가한다.

그럼 Shotest path의 Distance를 구하고, 그 경로를 어떻게 찾냐?

- 자기 자신으로 가는 것이나, 경로가 없는 것 = 무한대
- 자기 자신이 아니고, 경로가 존재하면 = i
- 또한 Shortest path에서 새로운 intermediate vertex k로 인해 더 짧은 경로를 찾았다면
prde[i,j] = k로 업데이트 한다.
▼ 아래를 보고 이해할 수 있다.
- 만약 모든 node에 대해 다 돌렸는데도 Pred[ i,j ] = nil 라면 , path가 존재하지 않는다는 의미이다.
- path가 존재하는데, intermediate 로 인해 업데이트 된 적 없다면 shortest path는 direct edge이다.

- pred[i,j] = i 라면 , shortest path 는 (i,j) edge이다.
- pred[i,j] = i 가 아니라면 , recursive compute로 ( i,pred[ i,j ] ) and ( pred[ i,j ] , j )
알고리즘 Ver.1
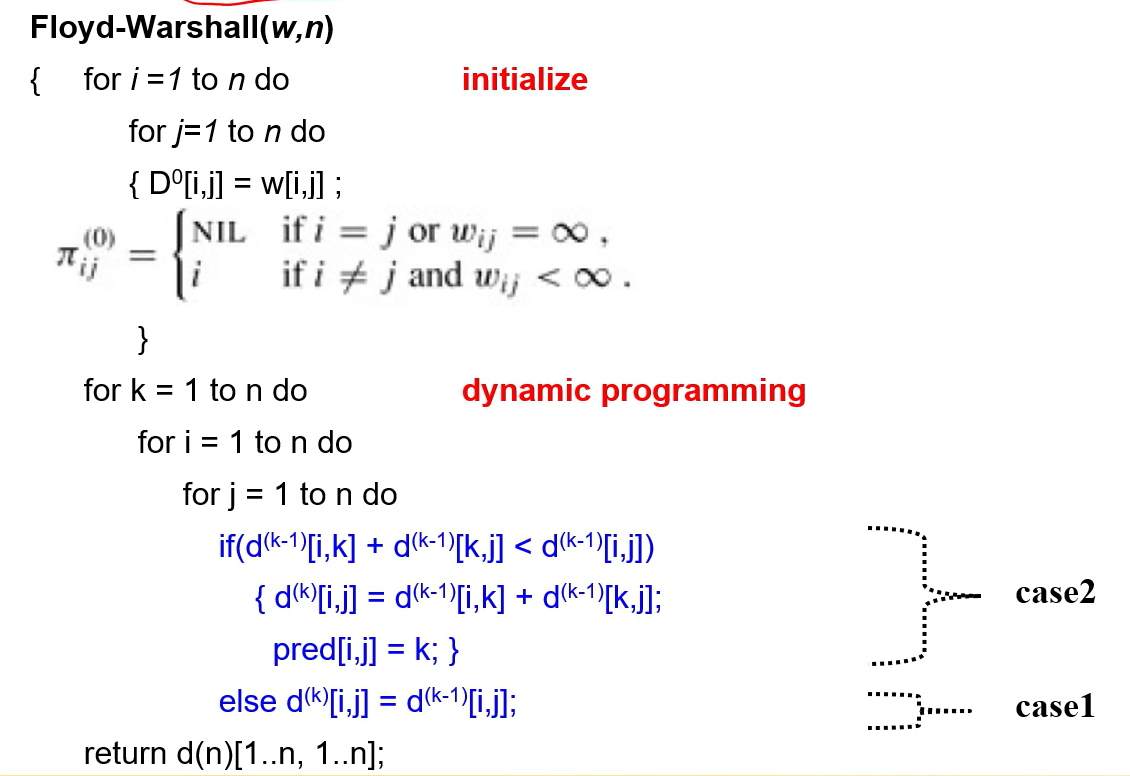
우선 윗부분은 초기화 단계이다.
for 안에 내용은 Intermediate vertex가 없을 때
Distance는 Edge weight으로 설정한다.

intermediate K 를 거치는 것과 그렇지 않은 것 중에 뭐가 더 작은지 판단.
▶ 거치는 것이 빠르면 distance 를 업데이트하고
▶ Pred 를 k로 업데이트한다.
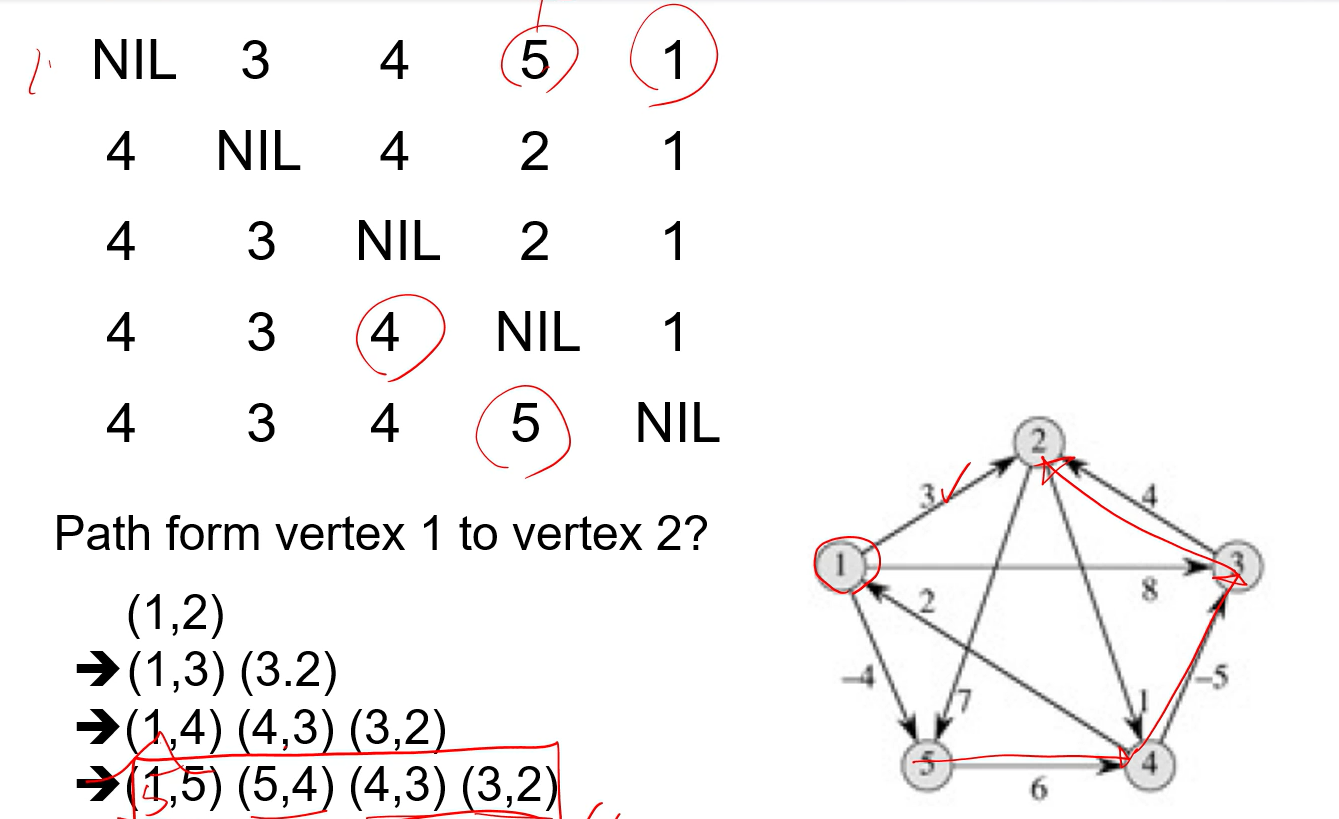
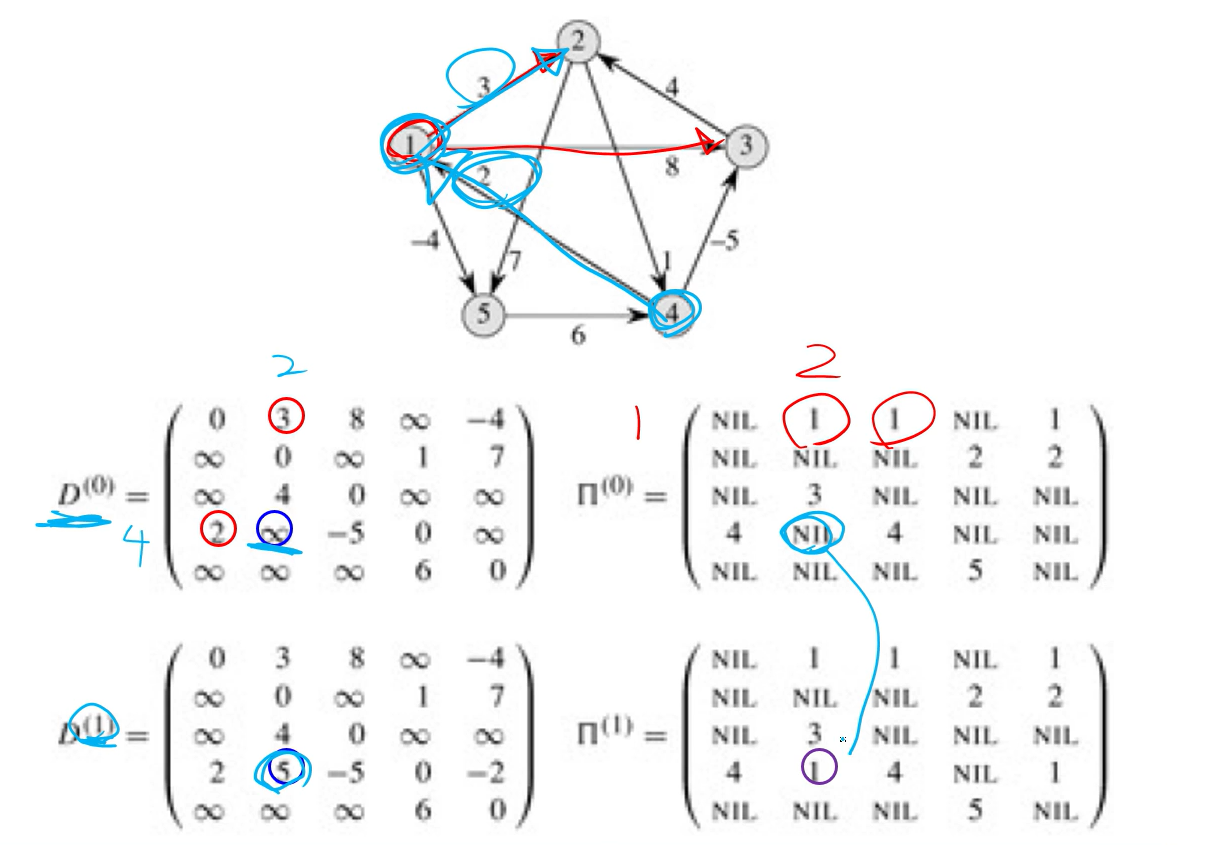
다음 Matrix에서 1에서 2로 가는 최단 경로를 구해보자.
1`~ 2의 Intermediate vertex는 3이다.
=13 , 32로 가야한다. [ 13, 32 ]
● 1~3 으로 가는 경로를 보자.
> 4가 Intermediate vertex이다.
= 14~ 43 이 되어야 함. [14 ,43, 32 ]
● 1~4 로 가는 경로를 보자
> 5가 Intermediate vertex이다.
15 54가 되어야 함 [ 15, 54, 43, 32 ]
Running Time : 세타(n^3) (n=Vertex로 해도 됨)
근데 이거 세타(V^2)으로 줄일 수도 있음
하나의 Intermediate Vertex가 생길 때마다 Matrix 하나씩 더 추가하는 게 아니라
n번째 단계를 만들기 위해 필요한 n-1번째 matrix 가 아니면 그 위에 덮는 것이다.
a matrix , b matrix있으면
1번 = a에 씀
2번 = b에 씀
3번을 만들 때는 b의 정보만 필요하므로 a위에 덮어 씀
4번을 만들 때는 3번의 정보 = a 의 정보만 필요하므로 b에 덮어 쓴다.
...반복
메모리에 관련된 문제를 해결할 수 있다.


왼쪽이 새로 만들어진 코드임.
if 에 (k-1)가 사라진다.
굳이 그걸 고려할 필요가 없이 돌면 되는 거라 그런 것 같다.
Transitive Closure
: Path가 존재하는지 알아내기
● 푸는 방법
: 모든 Edge의 weight를 1로 설정해두고 Floyd 알고리즘을 적용한다.
그 결과 , d<0보다 크다면 path가 존재한다는 뜻이고
d=무한대 라면 path가 존재하지 않는다는 뜻이다.

추가로 OR과 AND로도 풀 수 있다.
Edge의 weight 을 그대로 1로 매긴 뒤에
- 길이 없으면 0
- 길이 있으면 1로 초기화 시킨 뒤
i~j에 k가 intermediate인 vertex라고 했을 때
- 길이 k를 포함시키는 것이든, 아니든 존재하면 1
- 그렇지 않으면 0


풀어보자
자기 자신은 다 1로 해둔다.
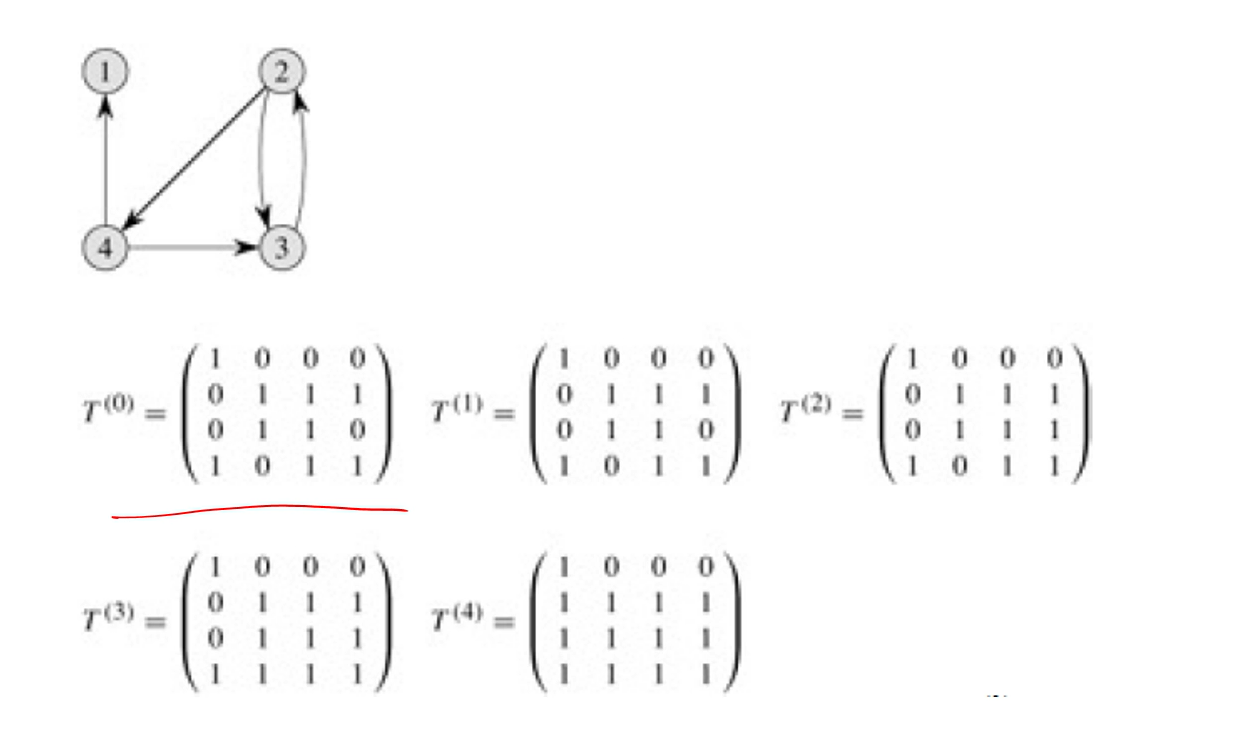
1빼고는 결국에는 서로 어디든 갈 수 있다.
(출처)
한동대학교 용환기교수님 - 알고리즘