[ 알고리즘 ] 20. Quick sort

: Sort에서 Divide and Conquer 를 사용하는 알고리즘

 

 

구간을 정하고 그 안에서 sort한다.

 

sort의 기준은 Pivot임.

 

이번에는 Pivot을 배열의 가장 마지막 원소로 지정한다.

 

 

x 가 pivot이라고 했을 때,

왼쪽은 x이하    오른쪽은 x이상 으로 분류한다.

 

 

옛날에 배웠던 건 Pivot element가 pivot이거나 , 처음 중간 끝 값 중에 가운데를 pivot으로 했다.

 

A = array

p = 첫번째 인덱스

r = 마지막 인덱스

 

이번에는 가장 오른쪽에 있는 element를 pivot으로 정한다.

검사는 → 이렇게 한 방향으로만 한다.

 

3번째 줄 : 그럼 처음부터 r-1까지만 검사하면 된다. 

 

4,5,6번째 줄 : 만약 현재 Index의 값이 Pivot보다 작으면, 

                    처음부터 올라오고 있는 i랑 현재 index랑 위치를 바꾼다.

 

 

Pivot보다 작으면 그냥 앞 쪽으로 보냄

 

 

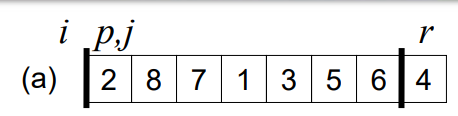
여기에서 시작하고

1,8 자리 교환

 

▼ 결과

 

 

i는 pivot보다 작으면 증가 ▶ j와 자리 교체

 

j는 매 반복마다 증가

i는 자기보다 작은 애를 만나야만 증가

 

반복이 다 끝나면 [ i의 자리+1 ] , 즉 pivot보다 작은 애들의 다음 index에 +1한 곳에 pivot을 넣는다.

그리고 Pivot을 기준으로 또 Recursive 하게 실행한다.

 

 

 

 

● Loop Invariant

 

 

Time complexity
세타(n)

 

● Worst case

 : Partition이 2개가 아니라 1개로만 나눠질 때 

   = Pivot이 가장 작은 값이거나 가장 큰 값이었을 때

 

 

이런 경우는 Elements들이 이미 Sort 되어있는 상태!!

 

 

 

세타 n을 cn으로 바꾸면 됨

 

 

Quick의

 

Worst case의 Time complexity

: 세타 (n^2)

 

 

Best case의 Time complexity

: 세타 (n lg n)

 

 

그렇다면 Average case는 어떨까?

Best case에 조금 더 가깝다고 한다.

 

Average case를 확인하기 위해서 볼 수 있는 Case는 2개가 있다.

 

• Randomize the input array   - 직관적인 분석 가능
• Randomized version of quicksort (Pivot을 random으로 정함)

 

 

Randomize the input array

 

- Balanced Partitioning

 

만약에 10개의 array에서 partition의 결과가 1:9 (혹은 9:1) 이라고 했을 때, 이도 Balanced라고 한다.

우리가 보여주려고 하는 건, 이렇게 Balance가 안 맞아보여도 

Time complexity는 세타(n lg n)이 나온다는 것이다.

 

 

이를 그림으로 그리면 다음과 같다.

 

여기에서 삼각형을 만들어 보면

 

 

우리가 가지고 있는 건 빨간색 삼각형이고 이 삼각형은

 

초록색 삼각형보다는 오래 걸리고

보라색 삼각형보다는 덜 걸릴 것이다.

 

그럼 그 중간값을 취하면 되는데  

 

매 Level은 cn

높이는 log 10의 n , log 10/9의 n이 있다.

 

삼각형의 넓이로 계산해보면

 

- 초록색 : 1/2 * cn * log 10 n

- 보라색 : 1/2 * cn * log 10/9 n

 

이를 Time complexity로 면 둘 다 세타 (n lg n)이다.

+ 99 : 1 balance로 나눠져도 똑같다.

 

 

- Produce a mix of "bad" and "good" splits

 

위 경우가 Bad split

이는 세타(n)

 

 

아래가 good split

이는 세타(n-1) = 세타 (n-1)

 

 

 

 

 

   Good Split이든 Bad Split이든 큰 상관이 없다.

 

 

a는 good bad split이 번갈아가면서 일어나고

b는 good split만 일어난다.

 

이 또한 average time complexity 가 세타(n lg n) 이다.

 

 

 

Randomized version of quicksort

Pivot을 Random으로 선택함

 

 

i에 random값을 넣어서 마지막에 넣고 (1,2번째 줄)

Partition 한다.

 

 

 

이 알고리즘의 Average Case를 분석해보자.

 

이렇게 나누었다면  왼쪽 : 오른쪽 Split의 경우의 수는 다음과 같다.

 

각각 이것들이 일어날 확률은?

1/n

 

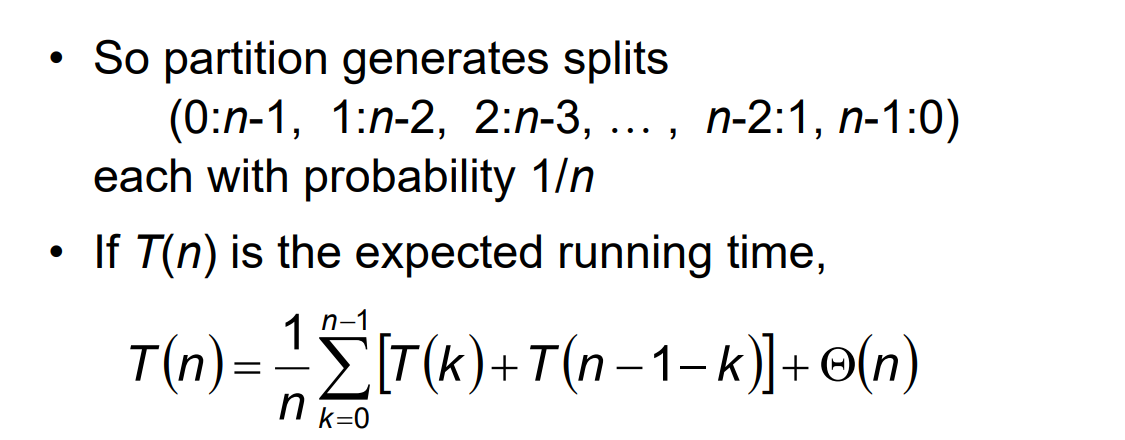
위 식은 아래를 간단하게 정리한 것이다.

 세타 (n) = partition 할 때 걸리는 시간

 

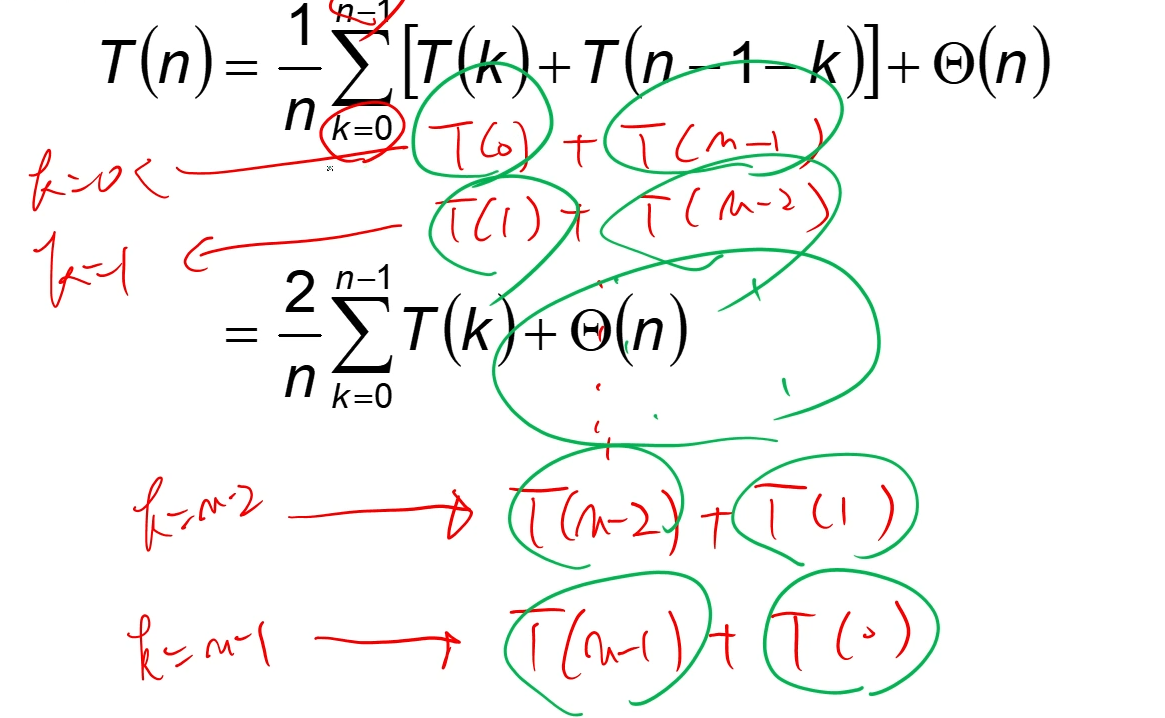
각각 2번씩 나온다. 

 

결과는

세타( n lg n )

 

정렬된 것만 세타 (n^2) 

그게 아니라면 평균적으로 세타 (n lg n)

 

 

세부 풀이법 ▼

k = a * (n lg n) 

 

 log k 에서 k가 0으로 수렴하면 = - 무한대

k 에서 k가 0으로 수렴하면 = 0

 

근데 k가 줄어드는 속도가 더 빨라서 0으로 취급 .

 

 

 

밑에 두 개는

 

이렇게 바뀐다.

 

 

 

(출처)

한동대학교 용환기교수님 - 알고리즘