오래 못 할 짓 하지 않기
[ 이산 수학 ] 20. 그래프 (4) 해밀턴 Paths , Circuits / 최단 경로 본문
728x90
해밀턴 경로 (Path)
= 그래프에서 모든 정점을 한 번만 지나는 경로
해밀턴 순환 (Circuit)
= 시작과 끝점이 같은 해밀턴 경로
= 모든 vertex를 한 번만 지나서 순회가 가능한 경

아래 3개가 해밀턴 경로인지 봐라
- G1 = ㅇㅇ 해밀턴 Circuit
- G2 = a가 막다른 길이라 Circuit은 안 됨.
대신 막다른 길에서 끝내서 Path로 만드는 건 가능.
( * 막다른 길이면 순회가 안 됨 b에서 a갔다가 순회하려면 다시 b를 밟아야 한다 )
- G3 = Circuit / Path 둘 다 안 됨
예제2)


Shortest Path Problems
이해해야 하는 거 : Dijkstra Algorithm
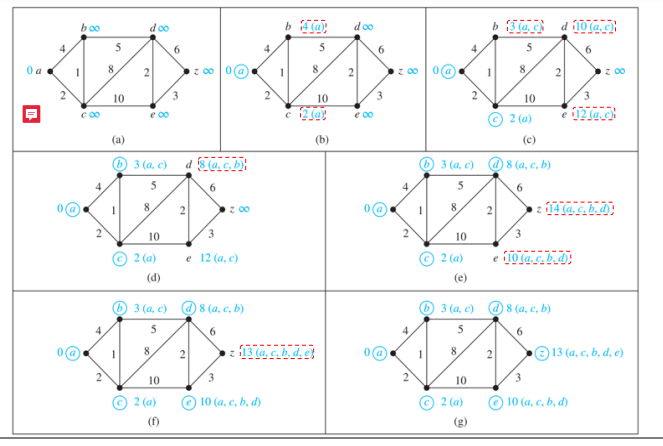
시작점에서부터 이어져 있는 가장 짧은 다리들로 이동하면 최단 경로가 된다.
모든 길을 무한대로 초기화해둔다.
1. a를 거쳐서 한 단계 다음으로 간 곳의 cost를 구한다. = b,c가 나옴
2. 1에서 구한 b,c 중에 작은 거를 고른다.--> a-c를 거쳐 한 단계 뒤에 있는 곳을 찾는다.
= b,d,e가 나옴
3. 2에서 구한 것 중에 짧은 경로 =b 이다. --> a-c-b를 거쳐 갈 수 있는 곳 중에 가장 짧 = d
4. a-c-b-d 에서 가장 짧 = e
5. a-c-b-d-e 에서 목적지로.
(참고)
https://www.youtube.com/watch?v=ERR7LFuhZq0
(해밀턴)
https://www.youtube.com/watch?v=IbFHEOpSvAI
(최단경로 2분20초부터)
'2학년 2학기 > 이산수학' 카테고리의 다른 글
| [ 이산 수학 ] 19. 그래프 (3) path / connected (0) | 2023.11.30 |
|---|---|
| [ 이산 수학 ] 18. 그래프 (2) (0) | 2023.11.28 |
| [ 이산 수학 ] 17. 그래프 (0) | 2023.11.24 |
| [ 이산 수학 ] 16. 관계(3) (0) | 2023.11.16 |
| [ 이산 수학 ] 15. 관계(2) (0) | 2023.11.13 |




