오래 못 할 짓 하지 않기
데구 총 정리 본문
Big - O Natition
-> Statements 보고 O( ? ) 구할 줄 알아야 함
--> ' 최고차항만 고려한다 ' 기억하기
스택 (Stack)
First in , last out
Push Pop <-- 탑에서 이루어진다.
대충 코딩 알고리즘은 알고있기
-- > Stack 응용 (할 줄 알아야함 시험에 나온다고 함) 연습하기!!
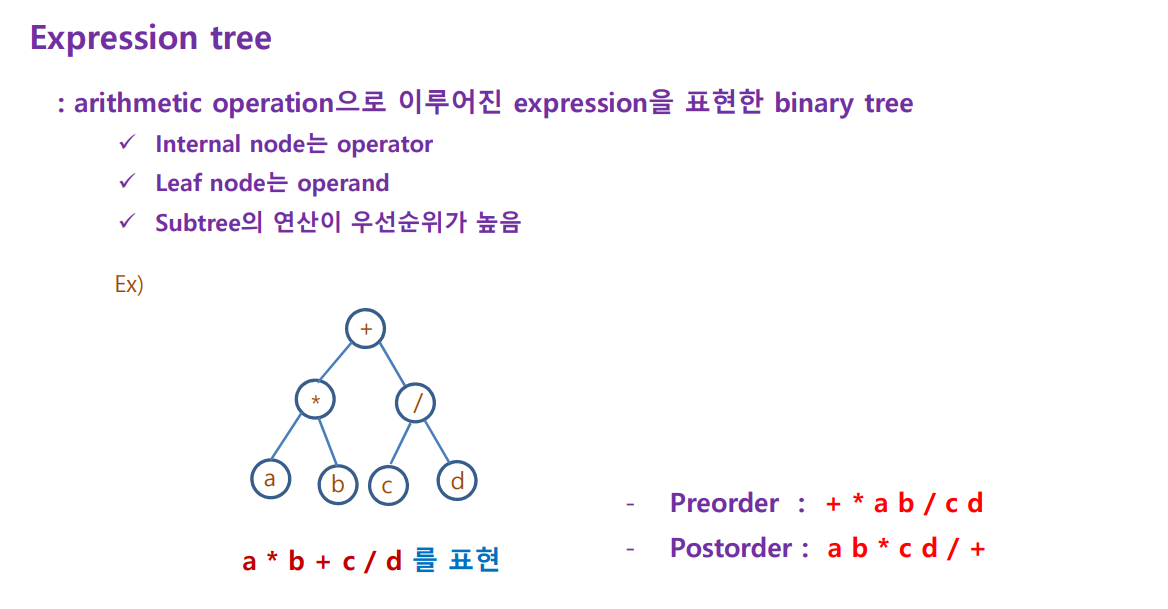
Expression (수식) 표현법
1 ) infix → a+b →부호가 숫자 2개 안(in)에
2 ) prefix → +ab →부호가 숫자 2개 앞(pre)에
3 ) post → ab+ →부호가 숫자 2개 뒤(post)에
## infix → prefix 하는 법 [ *문자가 나오는 순서는 식과 같음 ]
1) 식의 순서에 맞게 괄호를 친다.
2) 해당 괄호가 *열리는* = "("가 오는 곳에 괄호 안에 있는 부호를 넣는다.
ex) a+b*c = (a+(b*c)) = +a*bc / 데구4 종이 뒤에 있음
## infix → postfix 하는 법 [ *문자가 나오는 순서는 식과 같음 ]
1) 식의 순서에 맞게 괄호를 친다.
2) 해당 괄호가 *닫히는* = " ( "가 오는 곳에 괄호 안에 있는 부호를 넣는다.
ex) a+b*c = (a+(b*c)) =abc*+

큐(Queue)
First in, first out
- 구현법 : - front와 rear 값 증가 시, 끝 원소 후 첫 원소로 이어지도록 구현해야 한다.
→ rear=(rear+1)%SIZE
→ front=(front+1)%SIZE

- Empty , full 연산자 파악하기!
Empty → If(front==rear) / full → (front==rear)
문제점 : front==rear인 상황에서 더하려고 하면 꽉 찼다고 안 되고, 빼려고 하면 비었다고 안 됨
해결법 : 1칸을 안 쓰는 칸으로 만들어버린다.
empty는 그대로 front==rear일 때로 하고
full 연산자는(((rear+1)%SIZE) ==front) 일 때, 즉 rear에서 한 칸 더 갔을 때 front 일 때 (rear가 뒤에 있어야 함)
ADT ( Abstract Data Type )
안에 어떻게 돌아가는지 몰라도, 사용법만 알면 됨.
Class 구현 가능하거나 보고 뭔지 알 수 있어야한다고 하심.
+## Short Cirucit evaluation
:Evaluation 과정에서 결과값이 확정되면 나머지 뒤에 값들을 그냥 버리고 감
ex)
a=3;
b=4;
If((a++ == b ) or , and ~~~ ) 한 뒤에 끝나고 a와 b의 값 구하기 이런 거 있을 듯
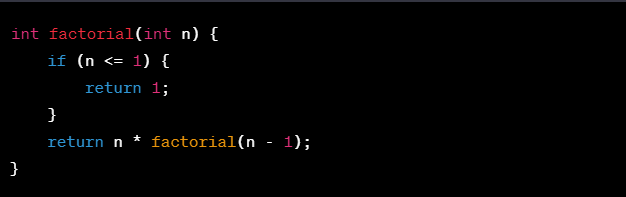
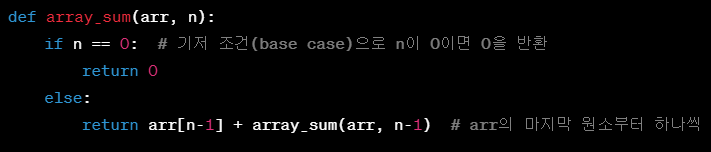
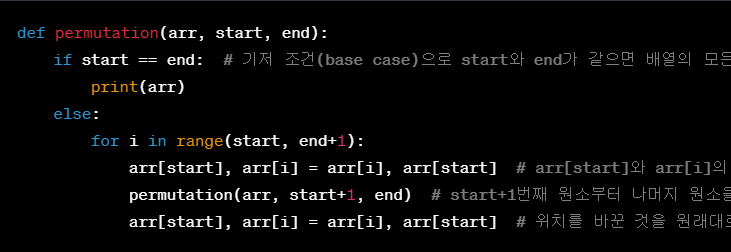
- Recursion --> Binary tree에서 쓰임.
- 자기 자신(Function body)을 Call 하는 것
- 반복이긴 하지만 for나 while이 아닌 call and return방식으로 반복
- 구성 요소 : Base case ( n==0 or n==1 일 때, ~~) + General Case
- 접근법 : 어느 단계의 값(n)은 한 단계 이전의 결과값(n-1)에서 어떤 차이가 있는지 분석하여 만든다.
: Base case -
: General case -



Pointer
ex) *p=나: / print(p) = 내 집 주소 / print(*p) = 나 (집에 사는 사람 = p라는 주소에 사는 사람)
→ 주소 값 을 다루는 data type
→ NULL을 가리키면, 아무것도 가리키지 않는다 라는 뜻
→ Scope 외에서 다루고 싶을 땐, 주소를 넘겨주고 pointer로 받으면 가능하다.
→ C에서는 malloc,free
C++ 에서는 a=new int[n]; / delete [a];
- Reference Parameter
1. sub(x) → void sub (int y)
2. 포인터 : sub(&x) → void sub (int *y) > 주소로 콜하고 포인터로 받음
3. Reference Parameter : sub(x) → void sub (int &y) > 변수로 콜하고 주소로 받음
2번 결과 = 3번 결과
→ 포인터의 주소에 가서 작업하는 기능을 사용하는 것

주소를 parameter로 받는 함수는 함수 콜이 끝난 뒤에도 변경된 값이 유지됨
Linked List
장점 : 크기, 메모리를 효율적으로 사용할 수 있다.
단점 : 다 Linked 가 되어있어서 Indexing이 불편하다. << a[80] 이게 안 됨
head = 새로 들어온 노드를 가리키는 포인터
tail = 가장 안 쪽에 박혀있는 노드 가리키는 포인터
- Add to head 알고리즘
1) 노드 생성 및 메모리 할당
2) 입력받은 내용 넣기
3) head 가 가리키는 노드를 같이 가리킨다 ( 내가 오기 전까지 처음이었던 놈)
4) head가 나를 가리키게 한다.
- Add to tail 알고리즘
1) 노드 생성 및 메모리 할당
2) 입력받은 내용 넣기
3) 노드가 NULL을 가리키게 한다 (tail에 넣으면 뒤에 가리키는 건 없으므로)
4)
4-1) tail이 NULL말고 가리키는 게 있다면 tail이 가리키고 있는 애가 방금 들어온 애를 가리킨다.
4-2) tail이 NULL이면, head도 NULL이라는 뜻이므로, head 가 p를 가리키게 한다.
5) 다 끝나고 나서 tail이 p(새로 생긴놈) 을 가리키게한다.
- Delete from head 알고리즘 <-- 정확히 delete보단 pop 개념에 가까움
1) 포인터 노드 , 그냥 노드 하나씩 생성
2) 포인터 노드로 삭제할 head에 있는 노드 잡아놓고 / 그냥 노드로 내용 복사해놓기
3) head 는 head가 가리키는 놈의 다음 놈으로 head= head->link
4) 포인터 노드로 delete
5) 삭제한 뒤에 head ==NULL 이면, tail ==NULL
6) 그냥 노드에 내용이 남아있는데 이걸 리턴.
for(p=NULL ; p!=NULL ; p->link) <<이거 모든 노드를 돌아볼 때 많이 쓰임
Linked list를 stack이나 Queue로 구현.
- Stack 은 top만 있음
= add_to_tail / delete_from_head
- Queue 는 front , rear가 있는데
노드 추가는 항상 rear ( tail = 가장 안 쪽) , 노드 delete(리턴) 은 front에서 한다.
= add_to_tail / delete_from_head임
invert
List_equal 보고 이해하기
Binary Tree
노드 수 - Lemma


- Traversal : 누락없이 모든 노드를 거치는 것
Inorder : 왼쪽 > 나 > 오른쪽 / [ 노드의 아래 ] 을 지날 때 인식함
Preorder : 나 > 왼쪽 > 오른쪽 / [ 노드의 왼쪽 ] 을 지날 때 인식함
Postorder : 왼쪽 > 오른쪽 > 나 / [ 노드의 오o른쪽 ] 을 지날 때 인식함
내려가다가 밑을 지난다고 하기 애매한 것들은 왼쪽이 있는지 확인하기.
왼쪽 없으면 본인 차례인 경우가 많음
Level order : 큐로 구현함
root가 Null이면 return
아니면 root를 queue에 넣음
- >다음을 반복
조건 : Queue가 empty가 아니면, (empty면 종료)
내용 : 1) queue에서 원소 하나(a) 가져옴
2) 그 원소 읽음
3) 읽은 원소의 왼쪽이 NULL이 아니면 queue에 넣음
4) 읽은 원소의 오른쪽이 NULL이 아니면 queue에 넣음
==> 요약하면 뺀 거 읽고, 그거의 (밑으로) 왼쪽 오른쪽 가져오는 거
- Expression
'2학년 1학기 > 데이터 구조 ( Data structure )' 카테고리의 다른 글
| 데이터 구조 11 (Heap) (0) | 2023.04.24 |
|---|---|
| 데이터 구조 10 (Traversal w/o recursion) (0) | 2023.04.13 |
| 데이터 구조 9 (Linked list 활용 , Trees) (0) | 2023.03.27 |
| 데이터 구조 8 (0) | 2023.03.23 |
| 데이터 구조 7 ( Functions, Reference parameter, Linked List ) (0) | 2023.03.20 |



