오래 못 할 짓 하지 않기
[ 컴퓨터 보안 ] 11. Cryptography : AES 2 본문
Original Design

저번에 봤던 AES Encryption은
각 Round와 Key를 Set로 묶어서 Inverse도 이론상 가능하다.
하지만 그 Round 안에서도 [ sub - shift - mix - round ] 를 뒤집어서 Decrypte한다.
순서가 Inv만 붙은 채로 평행하다.
( 사실 반대로 하는 거긴한다. )
Alternative Design

Subytes ➡️ Shift Rows 를 Inverse할 때는
InvSubByte ➡️ InvShiftRows 로 해도 Inversion이 가능하다.
암호화할 때랑 복호화 할 때 거치는 순서가 같다.
Inv만 붙인 채로 같은 순서로 하면 됨
따라서 최종적인 디자인은 아래와 같다
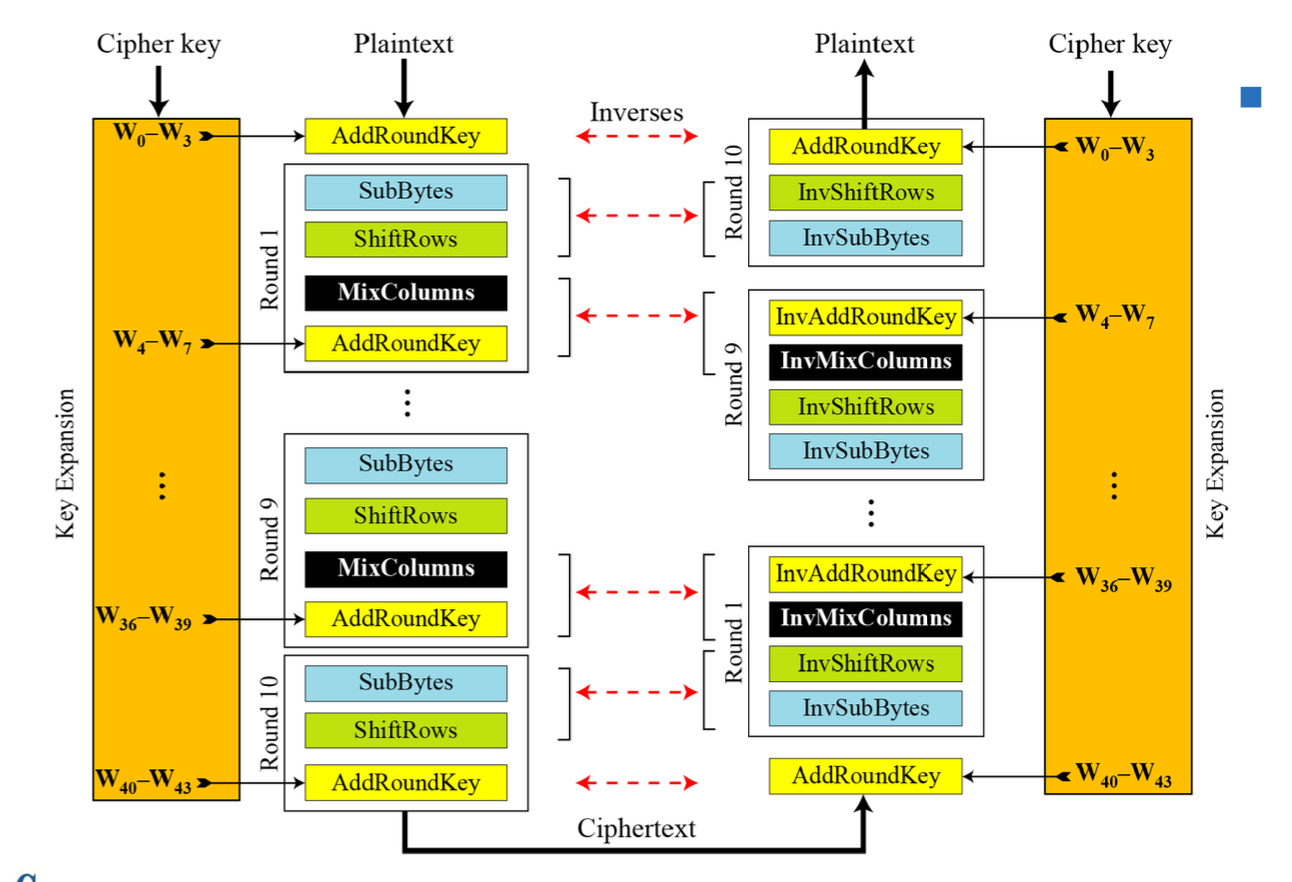
장점)
MixCoulumns 의 역할을 Key Expansion에 넣을 수 있기 때문에
복잡도(Complexity)를 조금 낮출 수 있다.
*근데 Original Design가 메인이니 그걸 보자!!
📌 AES 분석
- 보안적으로 DES에 비해 안전하다.
1) Brute-Force 공격에 안전하다.
➡️ Key size가 더 크기 때문에
2) Statistical 공격에 안전하다.
➡️ 어떤 알파벳이 많이 나왔나..볼 수 있는 것도 없기 때문에 안전함
3) Differential and Linear 공격에 안전하다.
➡️ 어떤 알파벳이 많이 나왔나..볼 수 있는 것도 없기 때문에 안전함
AES의 특징이나
DES랑 비교했을 때 어떤 게 다른지 알면 좋을 듯
Cryptography Mode
암호화/복호화를 시키는 것을 더 뜯어보자
안에는 여러가지 방법이 있다.
- ECB ( Electronic codebook )
- CBC ( Cipher Block Chaining )
- CFB ( Cipher Feedback )
- OFB ( Output Feedback )
- CTR ( Counter )
ECB
( Electronic codebook )
📌 특징
- Plain text를 여러 Block으로 쪼갠다.
- 항상 같은 Key를 가지고 암호화/복호화를 한다.
- 같은 Key를 사용하기 때문에, 같은 패턴의 Plain text는 암호화해도 같게 나와서 유추가 가능하다.
- 각 Block들은 서로 독립적이기 때문에 모두 패턴이 다르다면, 어느 하나가 털려도 문제없다.
- 한 쪽에서 Error가 발생해도 다른 Block에 영향이 없다.
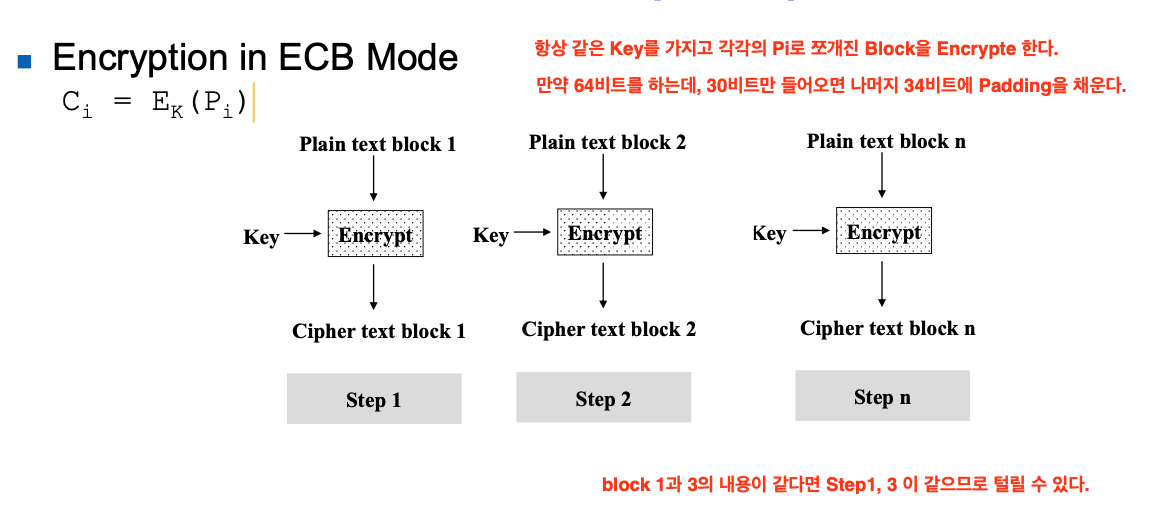
아래는 복호화
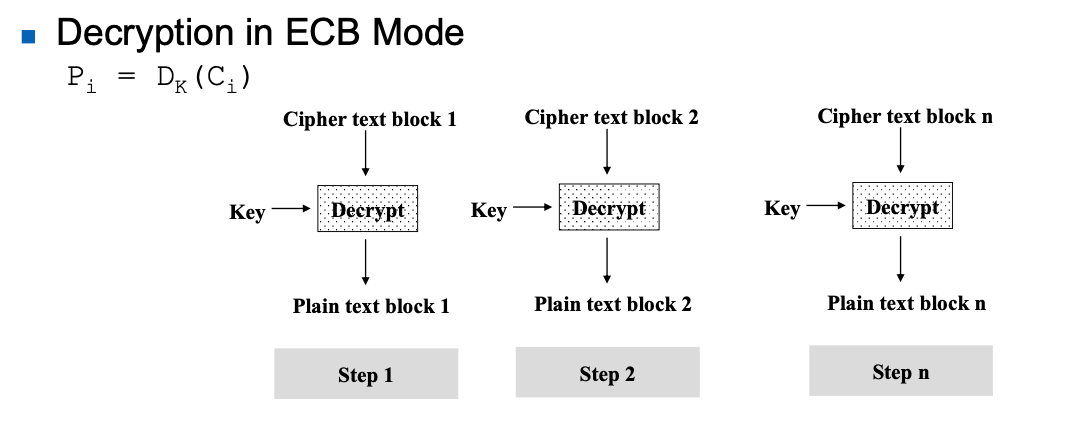
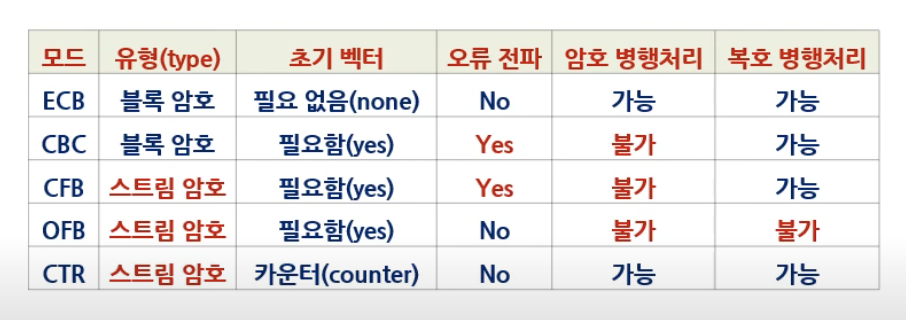
[ 공통으로 분석할 특징 ]
- Key Gen : 공통으로 사용하는 Key
- Propagation (error) : 발생하지 않는다.
- Parrael Processing : 가능하다 (서로 종속되는 게 없음)
CBC
( Cipher Block Chaining )
📌 특징
- Message를 여러 Block으로 쪼갠다.
- Encryption은 서로 Linked되어 있다.
- Initialization Vector를 사용한다.
- 각 Block들은 서로 독립적이기 때문에 모두 패턴이 다르다면, 어느 하나가 털려도 문제없다.

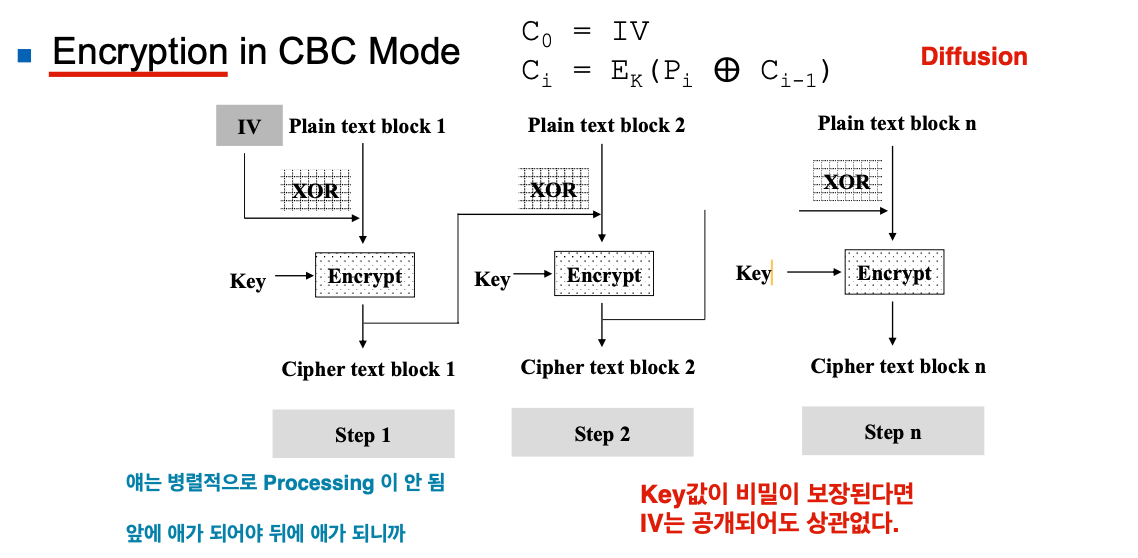
Plain text는 그냥 들어가지 않는다.
➡️ [ #무언가# ] XOR [ Plaintext ] 이런 식으로 들어간다.
* 첫 번째 Block : 무언가 = IV
* 그 외 i 번째 Block : i-1번째 Cipher Text
이렇게 해서 나온 값을 Key와 함께 Encryption Operation 한다.
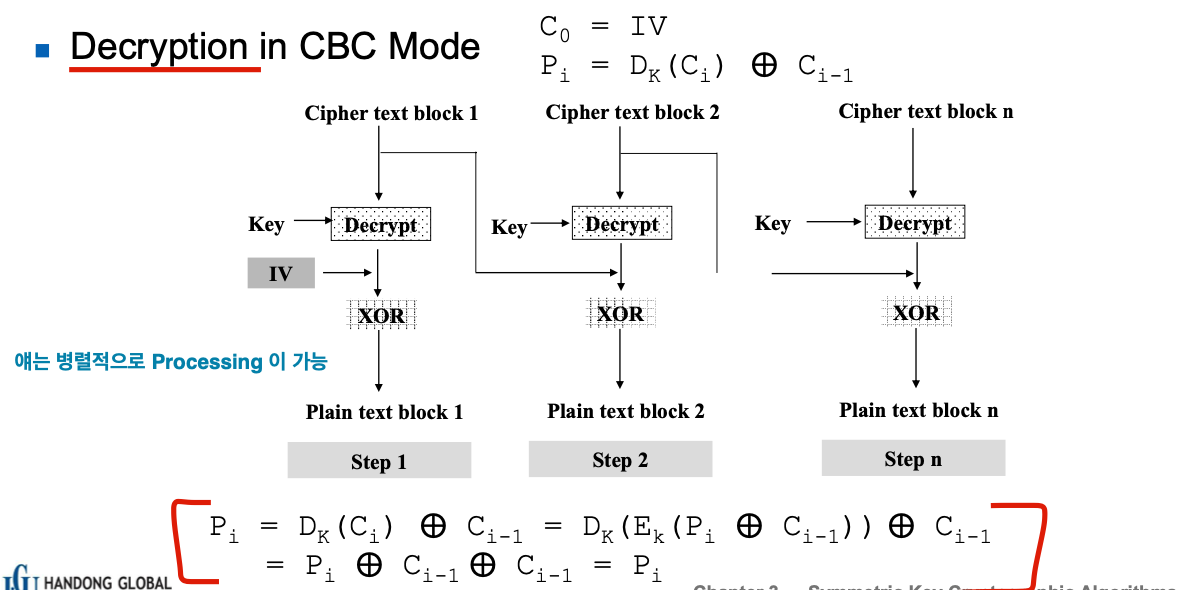
[ 공통으로 분석할 특징 ]
- Key Gen : 공통으로 사용하는 Key
- Propagation(error) : 복호화에서만 일어난다. 하지만 i번째에서 error 가 나면, 그 다음 block에만 영향을 끼친다.
- Parrael Processing : 복호화에서만 가능하다 ( 복호화는 그냥 주고 자기할 거 하는데, 암호화는 앞에 애가 다 해야 내가 받아서 시작)
CFB
( Cipher Feedback )

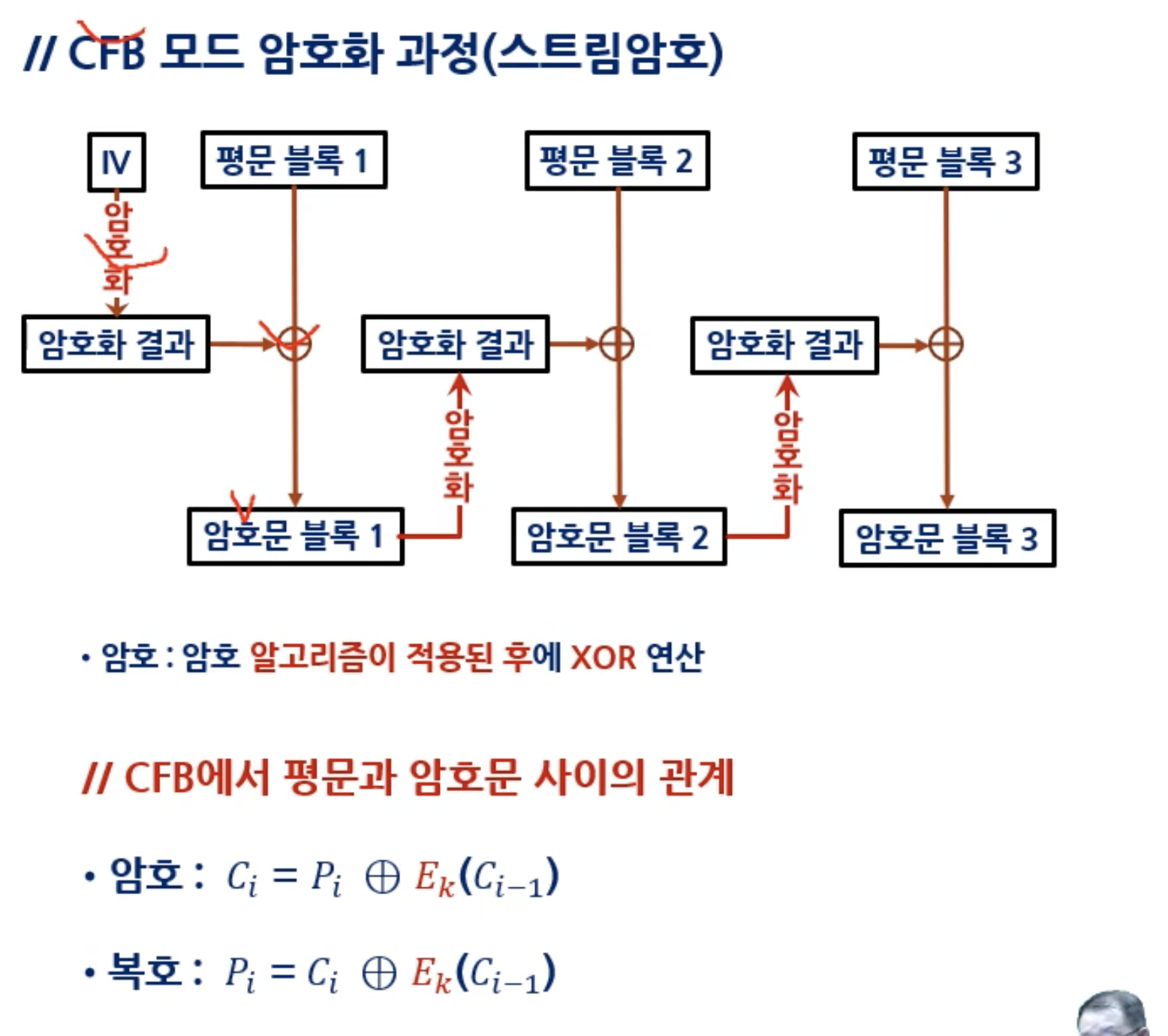
암호화 식을 한 번 보자.
현재 단계에서의 암호문 = [ 현재 단계 평문 ] XOR [ E(이전 단계 암호문) ]
이걸 이해하고 내려가면 보일 듯
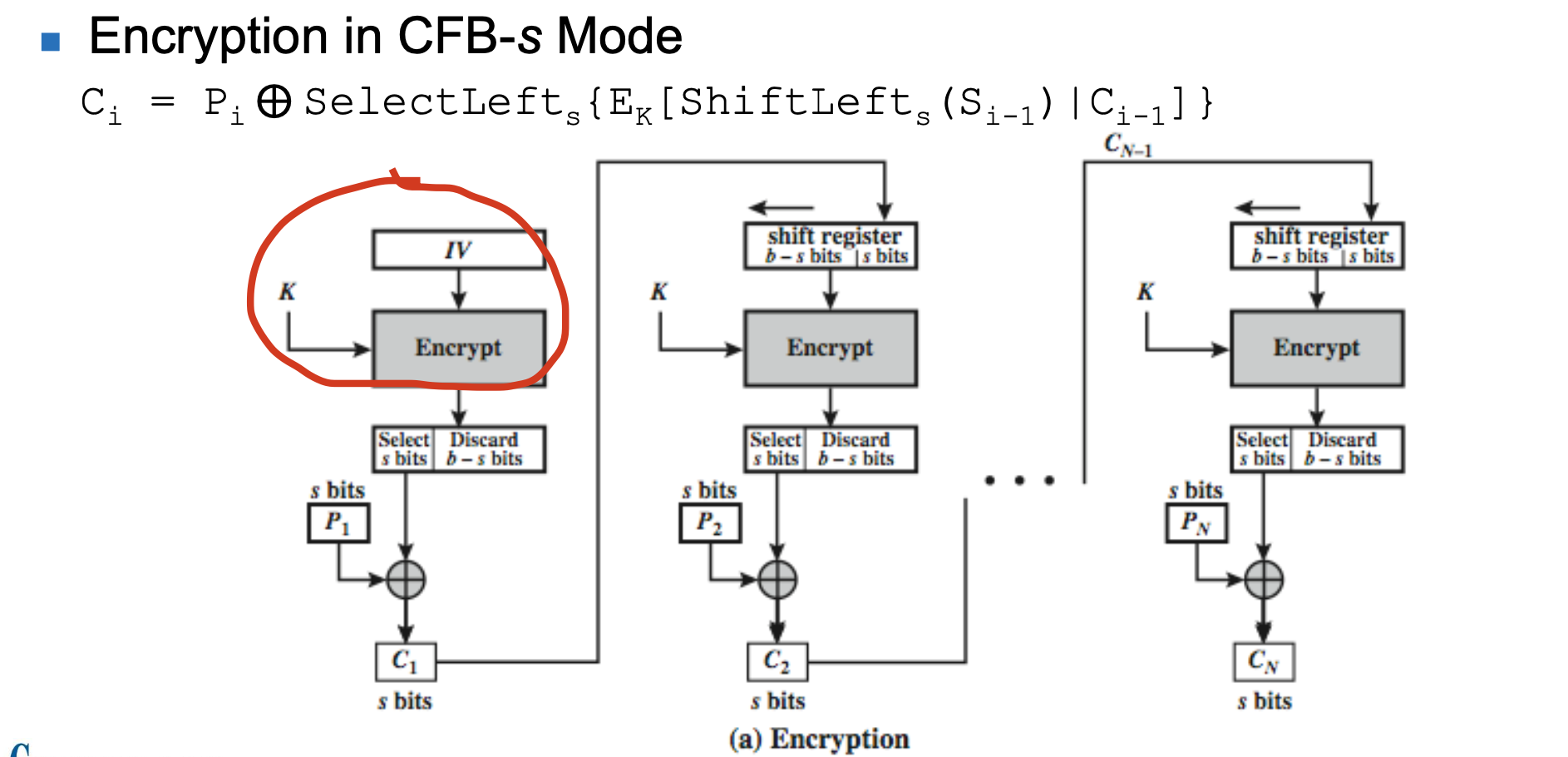
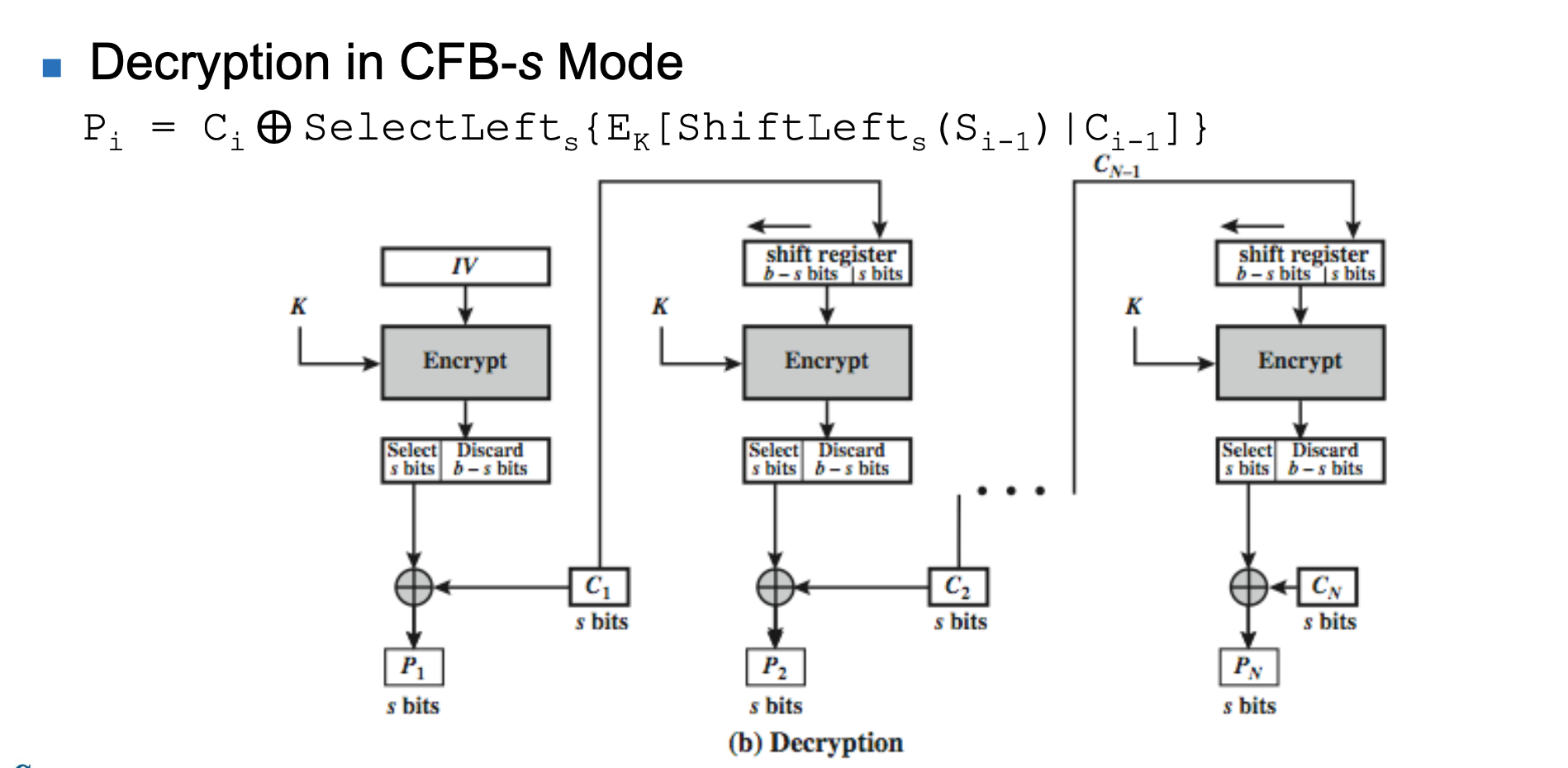
📌 작동 방식 (암호화)
(처음엔 이전 암호문이 없으니 IV로 시작한다.)
1) IV(OR C(i-1) ) 랑 K를 암호화한다.
2) 그렇게 해서 나오는 값에서 왼쪽에서 s개의 비트들만 가져온다.
3) 평문도 s개의 비트만 골라서 C1을 만든다. ( C1도 s개의 비트만 있음 )
그 다음 단계에서 다시 1~3을 반복하는데, IV가 아니라 이전 단계에서 나온 C를 사용한다.
> 똑같은 방법으로 하면 안 되니까 이 s 개의 bits를 오른쪽에서 Shift를 시키면서 넣는다.

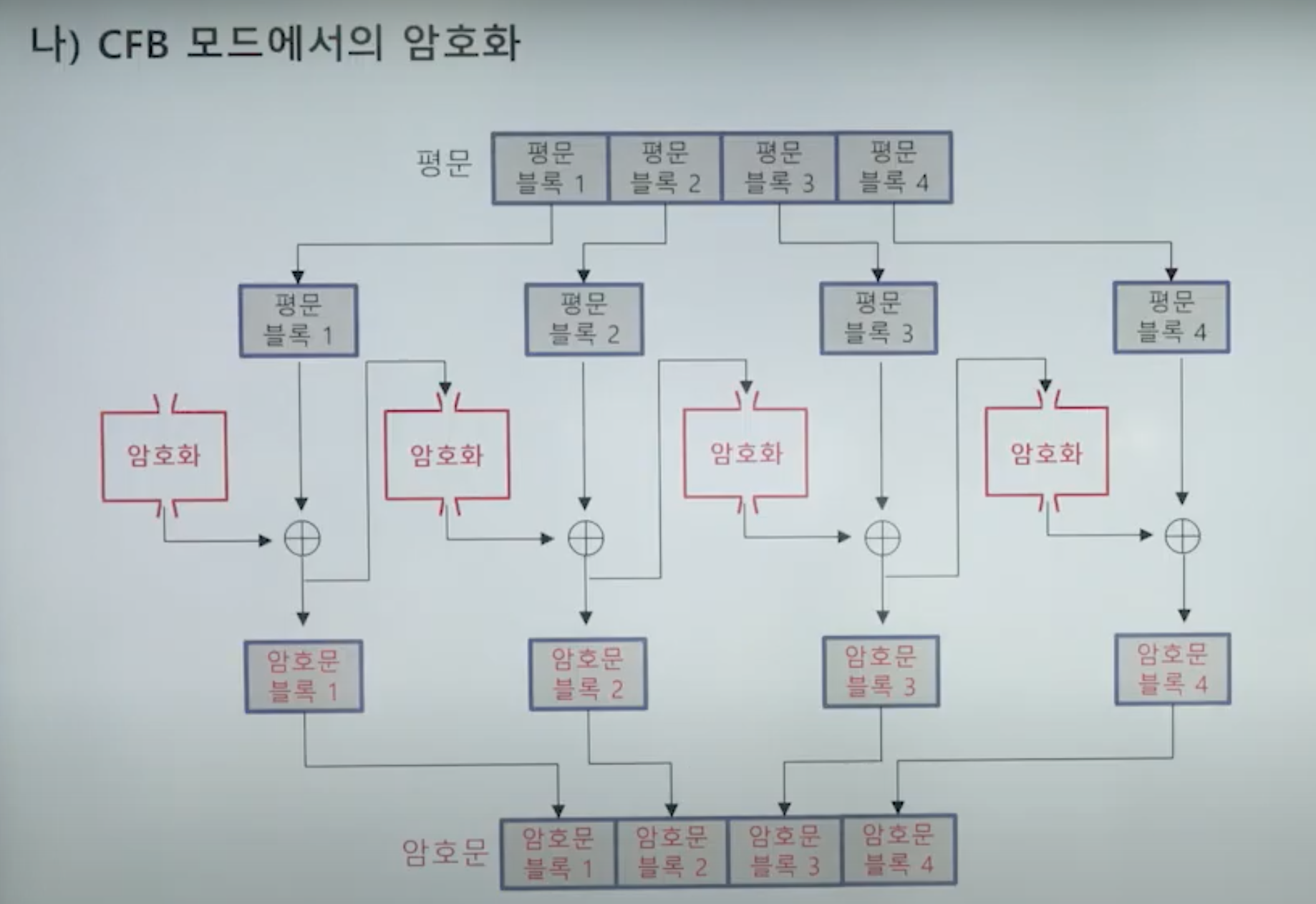
📌 특징
- Bit/Byte 단위로 들어오는 데이터 처리에 좋다.
- 복호화에서 Ci는 XOR 연산을 위해서도 사용되고, Encryption 될 때도 사용된다.
[ 공통으로 분석할 특징 ]
- Key Gen : 언급 없음
- Propagation(error) : Encrypt에서는 Error가 생기면 뒤에도 영향을 준다. 현재 만든 암호가 뒤에 영향을 끼치기 때문이다.
- Parrael Processing : 복호화에서만 가능하다 ( 복호화는 그냥 주고 자기할 거 하면 됨, 암호화는 앞에서 만들어진 결과를 받아야 함)
OFB
( Output Feedback )
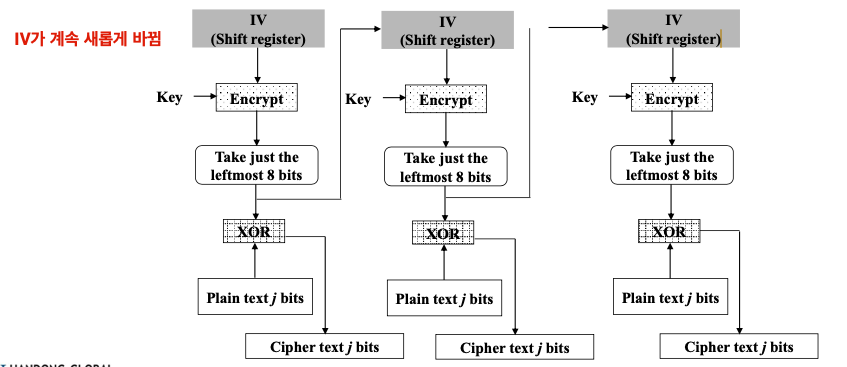
쉽게 펴보면 아래와 같다.
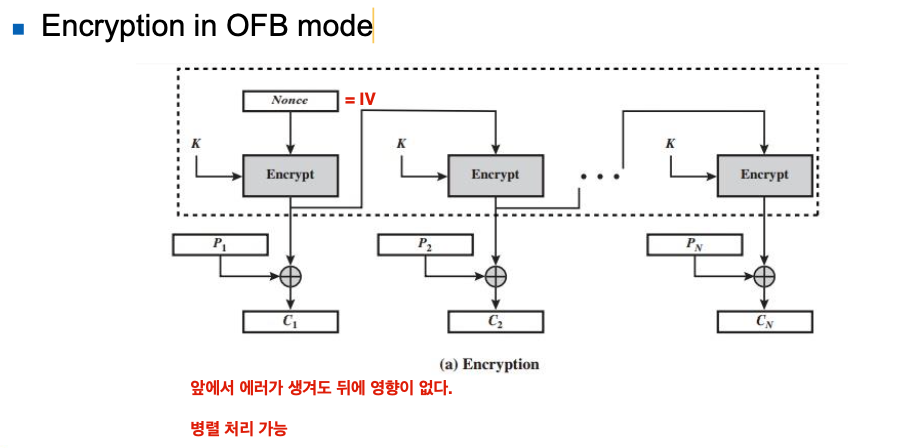
첫 Plain text에 대해서...
- IV랑 Key가 함께 암호화한다. 그렇게 암호화된 값을 A라고 하자
- [ A ] XOR [ Plain Text ]
그 이후엔
- A랑 Key가 함께 암호화한다. 그렇게 암호화된 값을 A라고 하자
A = 앞 Stage에서 E(Key,IV) 한 값, 처음엔 IV랑 하고,
그 뒤엔 E(Key,E(Key,IV)) 이런 꼴로 계속 덮어 쓰인다.
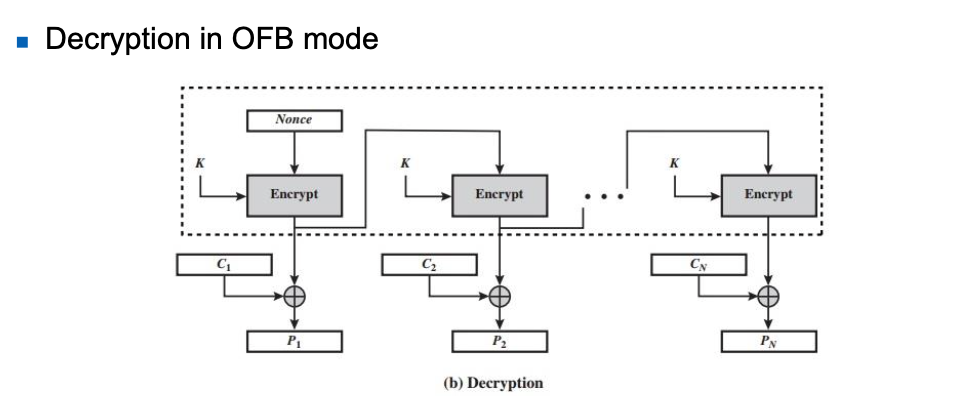
📌 특징
- CFB와 비슷하지만, Ciphertext는 이전 Bit들에 대해 Independent하다.
- Error Propagation 을 피할 수 있다.
[ 공통으로 분석할 특징 ]
- Key Gen : 공통으로 사용하는 Key
- Propagation(error) : Key와 IV에 대해서만 En/Decrypt하고 넘기기 때문에 text들에 대해서는 관여가 없기에 막힐 일이 없다.
- Parrael Processing : 병렬처리 가능 (Key , IV한 것만 지들끼리 바로바로 순식간에 다 하고 En/Decrpt하면 된다.
CTR
( Counter )

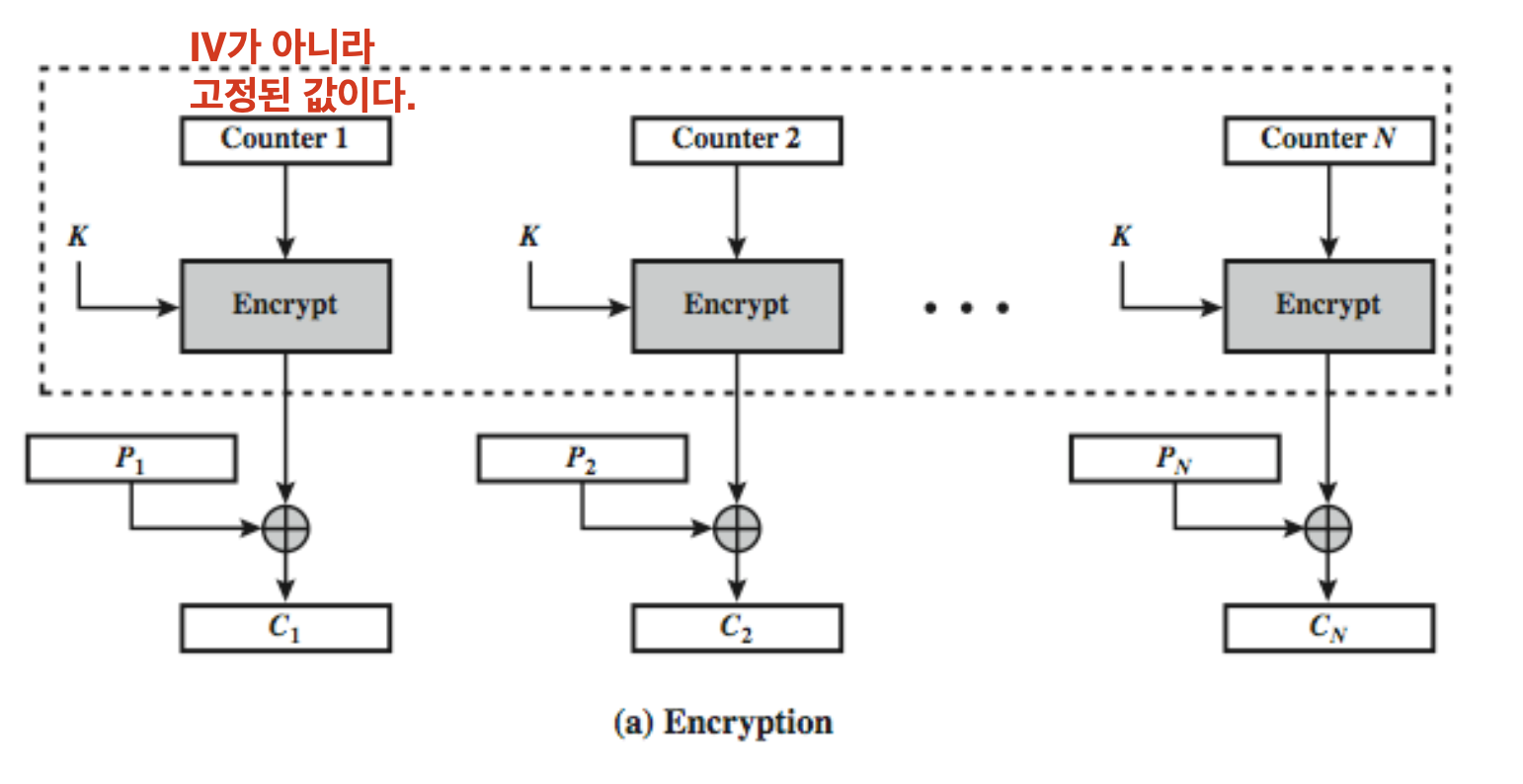
📌 특징
- 각 Counter마다 E( counter i , Key i ) 로 Encrypt 한다.
- 정말 서로 Independent함 ➡️ Error Propagation 을 피할 수 있다.
- Key랑 Counter 값을 다른 Counter에서 사용하면 안 됨. 재사용 XX
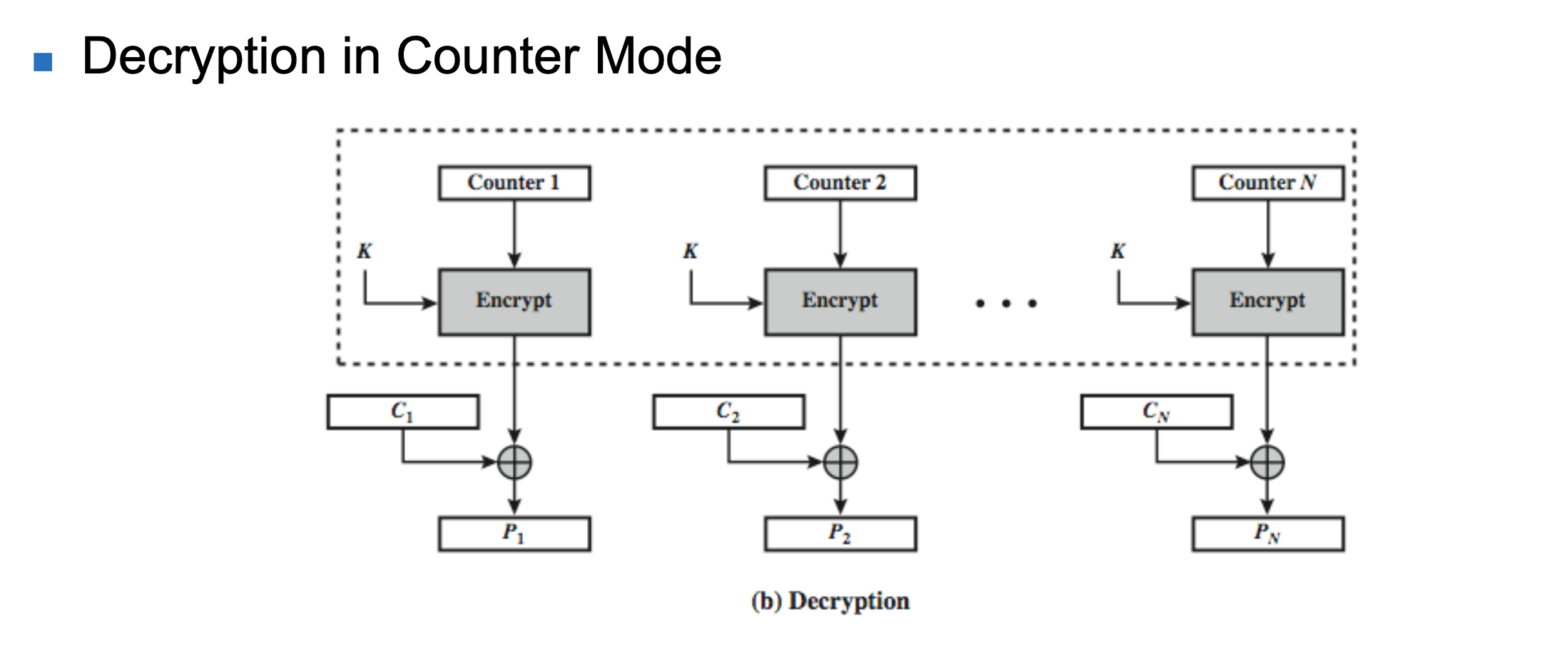
[ 공통으로 분석할 특징 ]
- Key Gen : 매 Count마다 다른 Key
- Propagation(error) : 서로 연결된 것 없이 Independent하기에 문제 없다.
- Parrael Processing : 서로 연결된 것 없이 Independent하기에 병렬처리 가능하다.
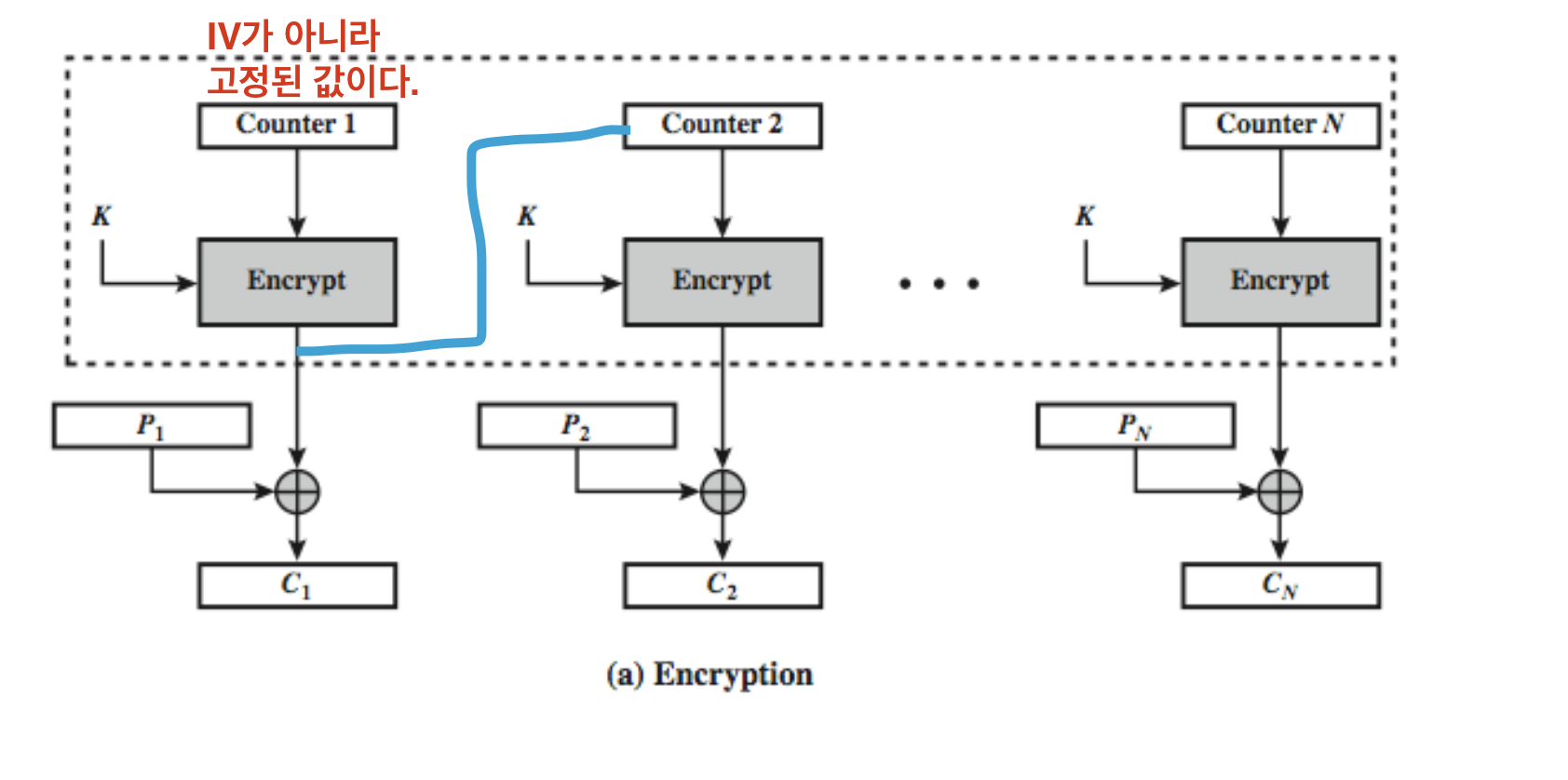
OFB에는 저 파란색 선이 있지만 Counter는 저걸 없앴다.
[ 중점적으로 알아야 하는 것 ]
Key Gen
Propagation
Parrael Processing 되는지 보면서 공부하기
+ 그림보고 뭔지 알기, 특징 설명하기

(출처)
한동대학교 고윤민교수님 - 컴퓨터보안
(참고)
https://youtu.be/6l5hhj224f8?si=oOfLeFF7CF-Fp7L2
https://www.youtube.com/watch?v=upqdlXSM8yE
(조금 더 자세함)
'3학년 2학기 > 컴퓨터 보안(Computer Security)' 카테고리의 다른 글
| [ 컴퓨터 보안 ] 13. Cryptography : Asymmetric Key - Message Digest (0) | 2024.11.05 |
|---|---|
| [ 컴퓨터 보안 ] 12. Cryptography : Asymmetric Key ( 비대칭키 ) (0) | 2024.11.01 |
| [ 컴퓨터 보안 ] 10. Cryptography : AES (0) | 2024.10.26 |
| [ 컴퓨터 보안 ] 9. Cryptography ( 이외 유닛 + DES ) (0) | 2024.10.22 |
| [ 컴퓨터 보안 ] 8. Cryptography 대칭키 ( + 비대칭키 ) (0) | 2024.10.15 |




