오래 못 할 짓 하지 않기
[ 네트워크 ] 20. Network layer (Control Plane) : Routing Protocol / Algorithm 본문
[ 네트워크 ] 20. Network layer (Control Plane) : Routing Protocol / Algorithm
쫑알bot 2024. 11. 25. 21:47Routing Protocol
📌Link State
: Node끼리 연결된 Link의 상태를 가지고 알고리즘을 통해 Routing하는 방법
- Dijkstra 알고리즘
➡️
특징 : Centralized 된 방식으로,
1) 모든 Node가 network Topology
2) 각각의 Link Cost는 모든 노드가 알고있다.
아래 코드도 러프하게나마 쓸 줄 알아야 할 것 같다.

- Init
>> 모든 Node에 대해 <<
1) v와 인접한 u에 대해서 D(v) = c(u,v)로 한다.
=(v와 u가 인접하다면, v까지의 거리는 u,v 사이에 있는 Link 의 Cost로 할당한다)
2) 만약 인접하지 않다면 D(v) = 무한대로 둔다.
- Loop ( 수행 횟수 = 노드의 수 )
:
1) Minimum인데 N'에 추가가 안 된 노드 w를 찾는다.
2) N'에 w를 넣는다.
3) w를 넣은 상태에서 D(v)를 업데이트한다.
* w와 인접함 && N'에 없어야 함
* 모든 Node가 N'에 들어갈 때까지 반복한다.

step 0에서 한 단계를 거쳤을 때, Least Cost는 x이다.
> x가 Minimum인데 N'에 안 들어있다.
> x를 N'에 넣고 다시 돌린다.
... 그렇게 계속 반복... 모든 노드가 N'에 들어갈 때까지 반복
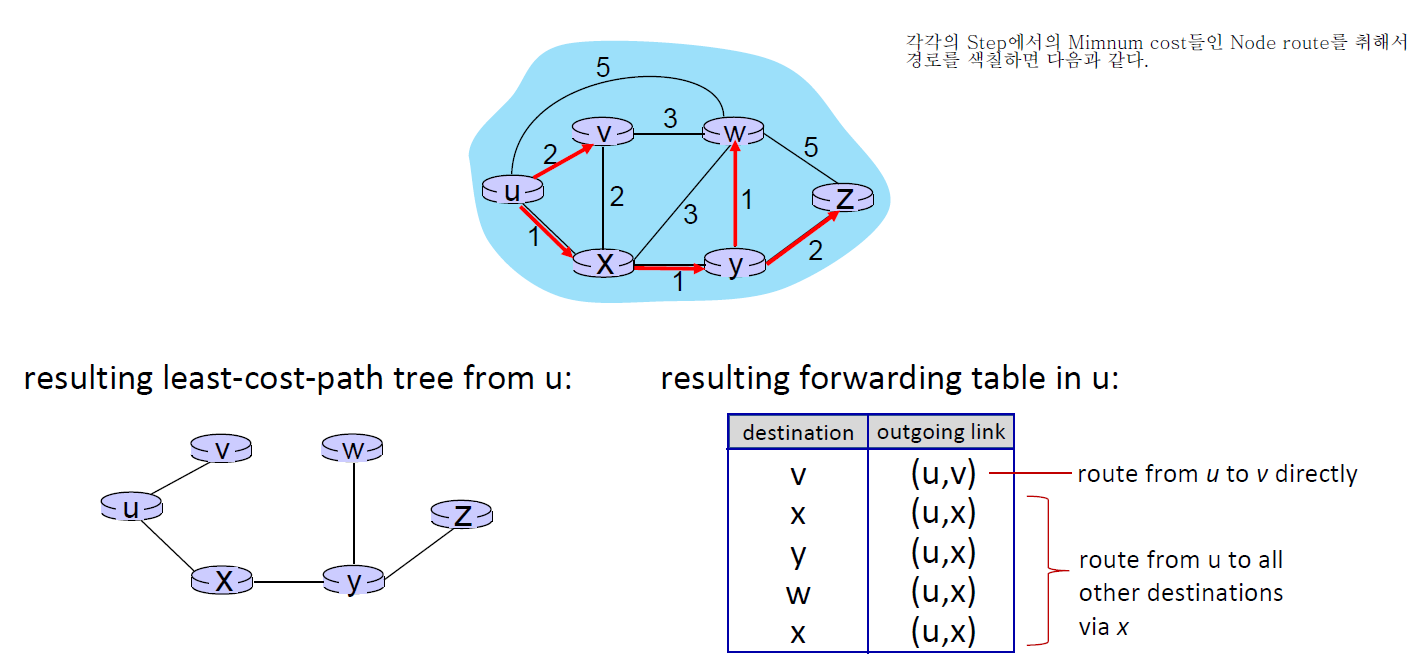
추가 예제 ↓
(더 이해하기 쉬움)

최대 Mix Heap을 통해서 O(n logn)의 Time Complexity를 뽑아낼 수 있다.
+ 각각의 Router가 꼭 Broadcast로 Link Cost를 모두에게 알려야한다.
[ 문제점 ]
- Oscillation Possible
* 링크의 비용은 통과하는 트래픽 양에 따른다.
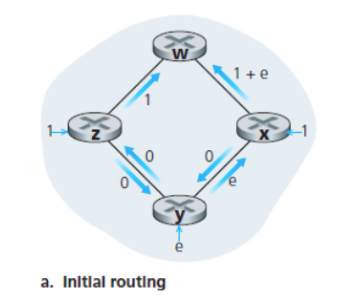
- w로 가는 y의 최소 경로 = min [ 시계 방향 = 1 / 반시계 = 1+e ]
- w로 가는 x의 최소 경로 = min [ 시계 방향 = 1 / 반시계 = 1+e ]
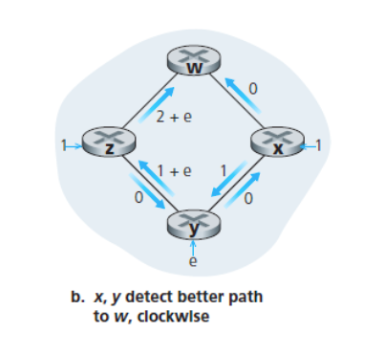
그렇게 실행시키고 업데이트를 한다면, 그 경로에 Cost가
- w로 가는 y의 최소 경로 = min [ 시계 방향 = e+1 / 반시계 = 0 ]
- w로 가는 x의 최소 경로 = min [ 시계 방향 = e+2 / 반시계 = 0 ]
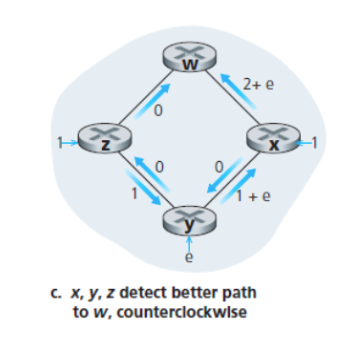
또 그렇게 실행시키고 업데이트를 한다면, 그 경로에 Cost가
- w로 가는 y의 최소 경로 = min [ 시계 방향 = 0 / 반시계 = e+1 ]
- w로 가는 x의 최소 경로 = min [ 시계 방향 = 0 / 반시계 = e+2 ]
마트에서 왼쪽 줄에 있다가 오른쪽 줄이 짧아보여서 모두가 다 같이 그 쪽으로 옮기면
왼쪽 줄이 짧아진다.
그럼 또 왼쪽 줄로 다 같이 이동...
...무한 반복
[ 해결법 ]
모든 라우터가 알고리즘을 동시에 돌지 않도록 한다.
각기 다른 시작 시간에, 같은 주기로 실행
📌Distance Vector = Bellman Ford 알고리즘

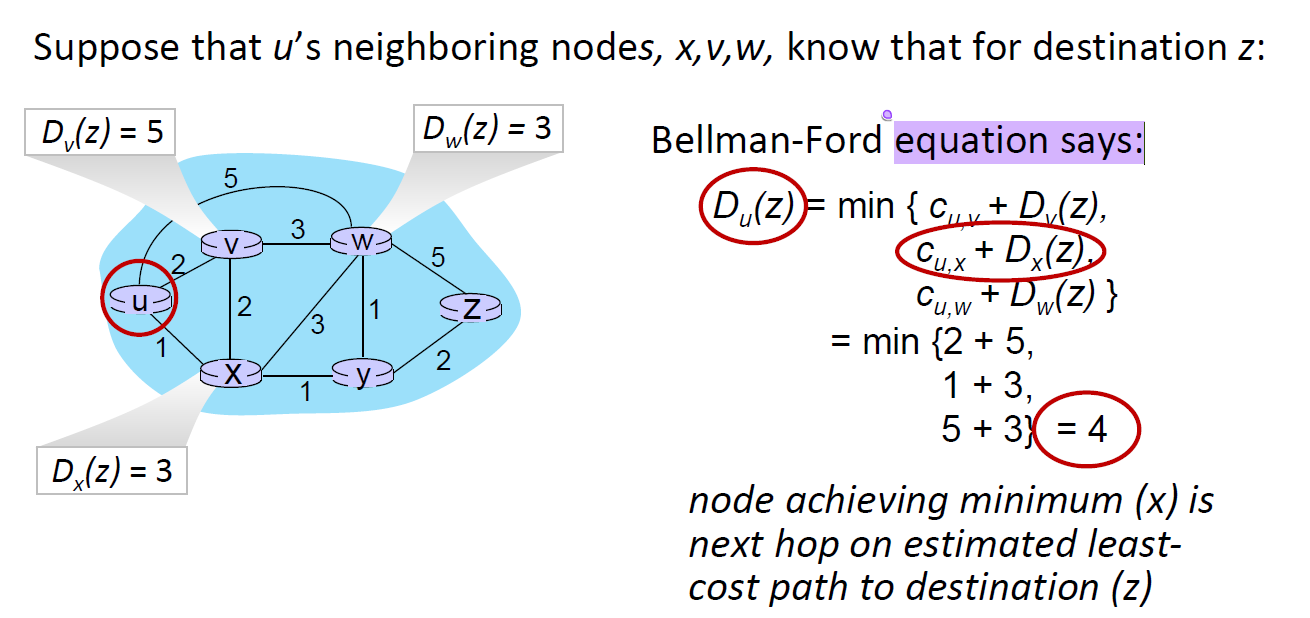
u에서 z까지의 최소 Cost는
1) u와 인접한 nodes = v,x,w를 선택
2) u-v cost + v-z까지의 거리
u-x cost + v-x까지의 거리
u-w cost + v-w까지의 거리
에서 가장 작은 값을 고른다.
ex) 1에서 3으로 간다면 c12 + D(2,3) 방식으로 간다.
위에 있는 Bellman Ford 방식을 각자 Node들에게 적용한다.
[ 거리 벡터가 변경되었다면 ]
1. 특정 Node가 자신과 이웃한 Node들과의 거리 벡터를
이웃들에게 보낸다.
2. 그걸 받은 이웃들도 자신의 거리 벡터를 갱신한다.

1. 변경이 있을 때까지 대기
2. 받은 정보를 기반으로 DV를 다시 계산한다.
3. 다시 계산한 DV를 주변에 알려준다.
... 이제 더 이상 변경이 없을 때까지 반복
예제)
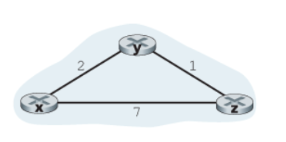
이렇게 Node 와 Cost가 있다고 해보자.
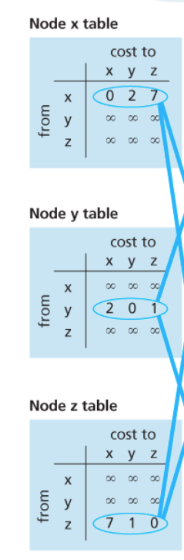
1. 각 노드별로 자신과 인접한 Node과의 Cost를 적는다. = 변경 발생
2. 변경이 발생했으므로, 주변 Node들에게 알린다.
3. Node들은 받은 정보를 기반으로 자신의 DV를 갱신한다.
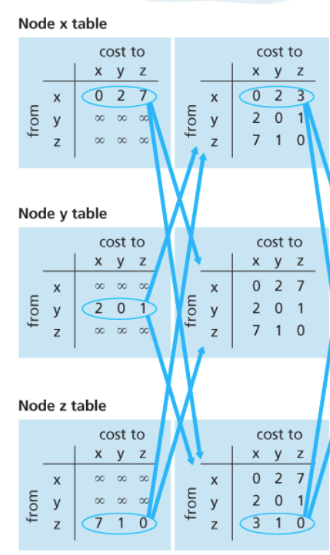
[ 갱신중 ]
x node가 y table을 받는다.
1. (x테이블 참고) x-y 까지 Cost는 2
2. (y테이블 참고) y-z까지 Cost는 1
=> x-z의 Cost는 3
이렇게 다 계산해보고 변동사항이 있으면 알려주고 받고 갱신하고 알려주고...반복
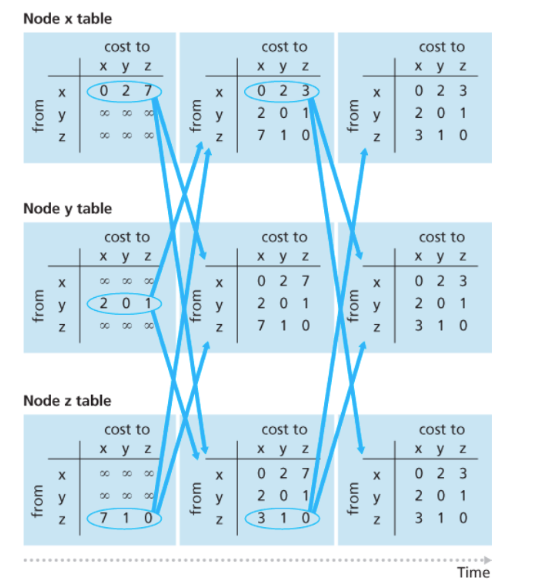
이거 꼭 해보기!!!!!!!!!!!!!!!!!

Case 1) Cost가 감소함
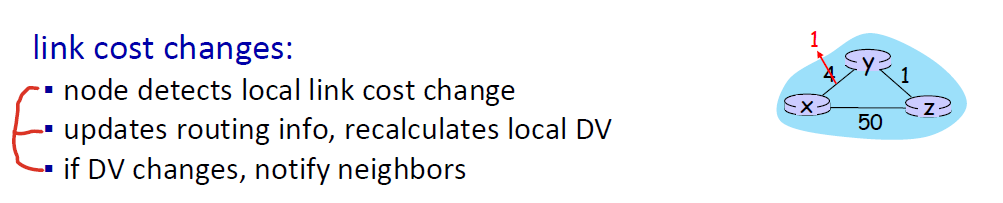
1. Node가 변화 감지
2. Routing Info를 업데이트 한 뒤, DV를 새로 계산한다.
3. 새로 계산한 DV가 이전 값과 다르다면, 주변 Node들에게 알린다.
위 같은 경우에는 x나 y가 본인들의 vector에 변화가 생기니까 동작을 해야함. y로 잡아보자.
t0= [ y가 변화 감지 ] + [ DV 업데이트 ] + [ 주변 Node에게 알리기 ]
t1 = [ z가 y의 Update를 들음 ] + [ x까지 가는 Least Cost 재계산 ] + [ 주변 Node에게 DV 알려주기 ]
t2 = [ y가 z의 Update를 들음 ] + [ Distance Table 업데이트 ] +
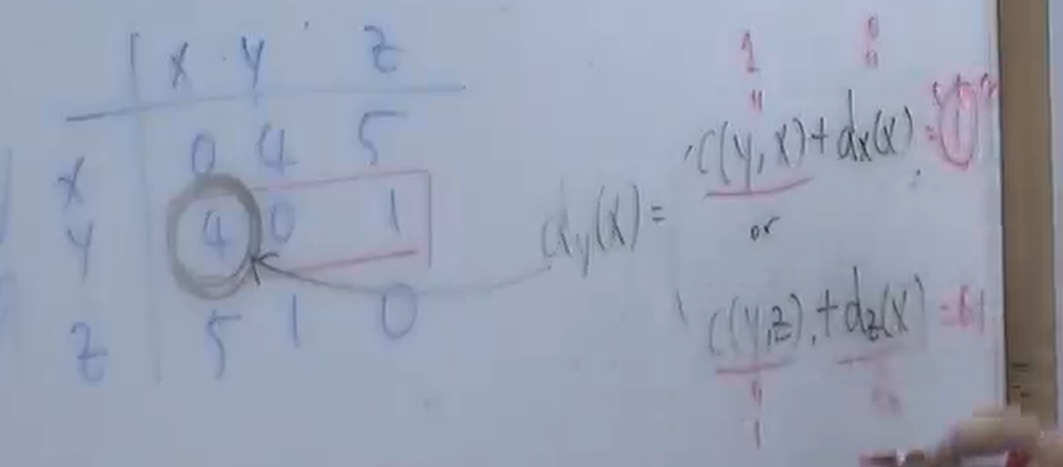
Cost 가 감소하는 경우에는 즉시 반영된다.
= 좋은 소식은 빨리 전달된다.
Case 2) Cost가 증가함
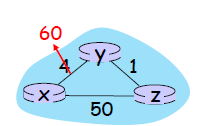
[ 1 ]
y에서 x로 가는 길 = [ y,x로 가는 cost ] + [ x에서 x로 ] = 60 + 0 = 60
or = [ y,z로 가는 cost ] + [ z 에서 x로 ] = 이미 알려져 있던 cost + 이미 알려진 z에서 x로 가는 cost = 1+5 = 6
➡️ y에서 x 까지 cost 가 6으로 업데이트되고, 주변 Node들에게 알려준다.
그 정보를 가지고 z는 x까지 가는 길은
[ z ,x로 가는 cost ] + [ x 에서 x로 ] = 50 + 0 = 50
[ z, y로 가는 cost ] + [ y 에서 x로 ] = 1+ 6 = 7
➡️ z에서 x 까지 cost 가 7로 업데이트되고, 주변 Node들에게 알려준다.
[ 2 ]
y에서 x로 가는 길 = [ y,x로 가는 cost ] + [ x에서 x로 ] = 60 + 0 = 60
or = [ y,z로 가는 cost ] + [ z 에서 x로 ] = 이미 알려져 있던 cost + 이미 알려진 z에서 x로 가는 cost = 1+7 = 8
➡️ y에서 x 까지 cost 가 8로 업데이트되고, 주변 Node들에게 알려준다.
그 정보를 가지고 z는 x까지 가는 길은
[ z ,x로 가는 cost ] + [ x 에서 x로 ] = 50 + 0 = 50
[ z, y로 가는 cost ] + [ y 에서 x로 ] = 1+ 8 = 9
➡️ z에서 x 까지 cost 가 9로 업데이트되고, 주변 Node들에게 알려준다.
... 이렇게 얘네가 업데이트 시키다가 50이 더 작은 값이 된다면 멈춘다.
Cost가 50이 될 때까지 돌아간다
Cost 가 증가하는 경우에는 천천히 전달된다.
= 나쁜 소식은 느리게 전달된다.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
(출처)
한동대학교 컴퓨터 네트워크
'3학년 2학기 > 네트워크 (Network)' 카테고리의 다른 글
| [ 네트워크 ] 22. Network layer : SDN (0) | 2024.11.28 |
|---|---|
| [ 네트워크 ] 21. Network layer (Control Plane) : Autonomous System (0) | 2024.11.28 |
| [ 네트워크 ] 19. Network layer : IPv6 / Routing Protocol (0) | 2024.11.21 |
| [ 네트워크 ] 18. Network layer : IP Addressing / NAT(Network Address Translation) (0) | 2024.11.18 |
| [ 네트워크 ] 17. Network layer : Router 내부 동작 (0) | 2024.11.14 |







