오래 못 할 짓 하지 않기
데이터 구조 14 본문
Spanning Tree
시작하기 전에 tree = 그래프의 일종 = cycle이 없는 그래프

Edge는 n-1개가 만들어진다.
Edge 개수 = Vertex 개수 -1 이니까
※ 원래 그래프에 있는 Edge만 사용 가능하다.
위 그래프 같은 경우엔 C -B 이런 건 안 됨
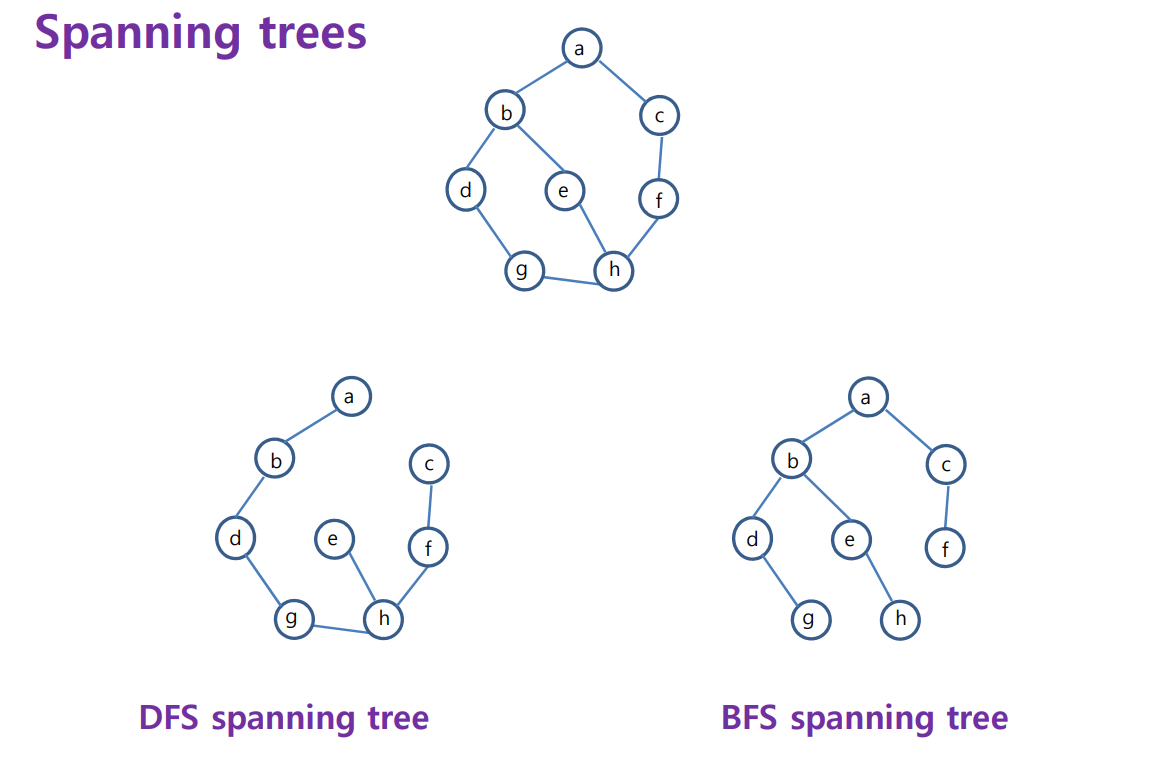
DFS , BFS 루트대로 만드는 Spanning tree도 있음
Biconnected Component
--> articulation point 를 갖지 않는 connected graph
+ articulation point
==> 해당 vertex가 삭제되면 원래 하나의 그래프가 두 개 이상으로 나눠지는 vertex.

위 사진에서는 C가 Articulation point임. C가 삭제되면 나머지 그래프가 둘로 나눠짐
Minmum Cost Spanning Tree
--> Weighted graph에서 cost의 합이 최소인 spanning tree 를 찾기
- 크루스칼 알고리즘
1. Edge 들을 Cost 순서대로 Sorting.
2. 가장 작은 Cost Edge부터 가져온다.
3. Cycle이 안 만들어지면 선택
4. Edge가 (n-1)개 선택되면 끝

--> 낮은 코스트들 먼저 연결하고, 하다가 밑에서 가운데 보면 4를 선택하면 Cycle이 되어서 선택 안 함
- 프림스 알고리즘
1. 시작 vertex 선택.
2. 현재 만들어진(이어진) connected component와 외부로 연결된 edge중 cost가 가장 작은 걸 선택
3. (n-1)개 선택하면 끝


1. 시작은 a.
2. a에서 외부로 연결된 edge중에 가장 cost가 적은 건 a-b(2)이다.
3. 선택.
4. 그 다음 a-b < connected component 에서 외부로 가는 edge는 7 8 4 3 이 있다.
5. 이 중에서 cost가 가장 낮은 3을 선택
(계속 반복...)
6. edge가 n-1개가 되면 종료
- 솔린 알고리즘
1. 각 vertex를 개개인으로( = 서로 다른 connected component) 둔다.
2. 각 connected 에 대해 최소 cost인 edge 선택
3. 전체가 1개가 되면 끝 (이거도 edge가 n-1개 )

a에서 가장 적은 cost인 edge = 2
b " " = 2
c " " = 5
d " " = 1
e " " = 1
f " " = 5
g " " = 6
이렇게 하면 이어지는 것들이 있다.
여기에서 한 번 더 반복
a-b 에서 가장 적은 cost인 edge = 3
c-f 에서 "" "" = 7
d-e-g 에서 "" "" = 3
Shortest Path
Weighted Graph에서 특정 vertex 에서 다른 모든 vertex 에 이르는 최단 거리 path

알고리즘 :
시작 전 -> Adjacency matrix 에서 기준 vertex에 해당하는 행을 초기값으로 설정
진행 -> 다음을 (n-2)회 반복
1. 아직 방문하지 않은 vertex중 가장 가까운(cost가 낮은) vertex 선택
2. 해당 vertex를 거쳐서 가는 path가 현재 알려진 path보다 짧으면 짧은 거로 수정
예 ) 포항을 시작으로해서 path를 분석!


Matrix가 이렇게 있고, 포항은 v4이므로 v4 행을 가져온다.
1. 아직 방문하지 않은 vertex중 가장 가까운(cost가 낮은) vertex 선택
--> 하면 V 7으로 먼저 간다.

2. 1에서 고른 곳을 거쳐서 가는 것이, 현재 알려져있는 경로보다 짧으면 수정한다.
1에서 고른 곳 : v7 /
v7에서 갈 수 있는 곳 : v6
--> 들르지 않았던 v6까지 간다. v7->v6 ( 55 )
그럼 부산까지 가는 길은 145에서 120이 될 수 있으니 120이 최단경로임.
바로 업데이트
한 번 반복 끝

2번째 수행 ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
1. 아직 방문하지 않은 vertex중 가장 가까운(cost가 낮은) vertex 선택
--> v3으로 간다 v4->v3(70)
2. 1에서 고른 곳을 거쳐서 가는 것이, 현재 알려져있는 경로보다 짧으면 수정한다.
1에서 고른 곳 : v3 /
v3에서 갈 수 있는 곳 : v0,1,2,5
--> v3에서 방문하지 않은 곳은 v3-> v0,v1,v2,5이다.
각각 v4 -> v3 -> v0,1,2,5 를 구할 수 있다.
- v4 -> v3 -> v0 (70 + 360 = 430)
- v4 -> v3 -> v1 (70 + 140 = 210)
- v4 -> v3 -> v2 (70 + 160 = 230)
- v4 -> v3 -> v5 (70 + 220 = 290)


3번째 수행 ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
1. 아직 방문하지 않은 vertex중 가장 가까운(cost가 낮은) vertex 선택
v6 = (120 = v4 -> v7 -> v6)에서
갈 수 있는 곳 (간 적 없는 곳)은 v5이다.
2. 1에서 고른 곳을 거쳐서 가는 것이, 현재 알려져있는 경로보다 짧으면 수정한다..
근데 v4 -> v7 -> v6 = 120 + 250 = 370이고,
v4 -> v3 -> v5 = 70 + 220 = 290이므로, 변화는 없다


4번째 수행 ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
1. 아직 방문하지 않은 vertex중 가장 가까운(cost가 낮은) vertex 선택
120까지 갔으니 그 다음으로 작은 것은 210 인 v1이다.
v1에서 갈 수있는 곳은 v0,v5 (v1에서 온 거라서 X)
2. 1에서 고른 곳을 거쳐서 가는 것이, 현재 알려져있는 경로보다 짧으면 수정한다..
v1 -> v0 = 210 + 160 = 370 이고, v0 원래 430 보다 370이 더 작으므로 370으로 변경
v1 -> v5 = 210 + 170 = 430 이라 원래 290보다 크므로 변경 X


5번째 수행 ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
1. 아직 방문하지 않은 vertex중 가장 가까운(cost가 낮은) vertex 선택
v1 - 210 까지 했으니 그 다음은 v2 - 230으로 시작
v2에서 갈 수 있는 곳은 v0 (v3는 거기에서 온 거기 때문에 안 됨)
2. 1에서 고른 곳을 거쳐서 가는 것이, 현재 알려져있는 경로보다 짧으면 수정한다..
v2 -> v0 = 230 + 120 = 350 이므로 v0이 370인데 그거보다 작으므로, 350으로 수정


6번째 수행을 하려고 보니까 v0으로 오는 것들은 다 왔기 때문에 방문 안 한 곳이 없음
n-2에서 -2는 시작하는 곳은 자기한테 오는 게 없고 , 마지막은 갈 수 있는 곳이 없기 때문에 -2를 한다.
Bellman and Ford algorithm
- 기준 vertex (v)에서 다른 모든 vertex 에 이르는 shortest path 를 찾기
- 방법 :
모든 edge에 대하여 다음 과정을 ( n-2) 회 반복
== > 그 edge를 거치면, 현재 알려진 length보다 짧아지면, length를 수정
for (k = 2; k <= n-1; k++)
for (each edge (v1, v2) in the graph)
if (dist[v2] > dist[v1] + cost[v1][v2] )
// v1을 거쳐서 v2로 가는 게 v2로 바로 가는 것(혹은 현재 가장 cost가 적다고 알려진 path) 짧으면
dist[v2] = dist[v1] + cost[v1][v2];
// v2까지 가는 길을 v1을 거쳐서 가는 거로 바꾼다.
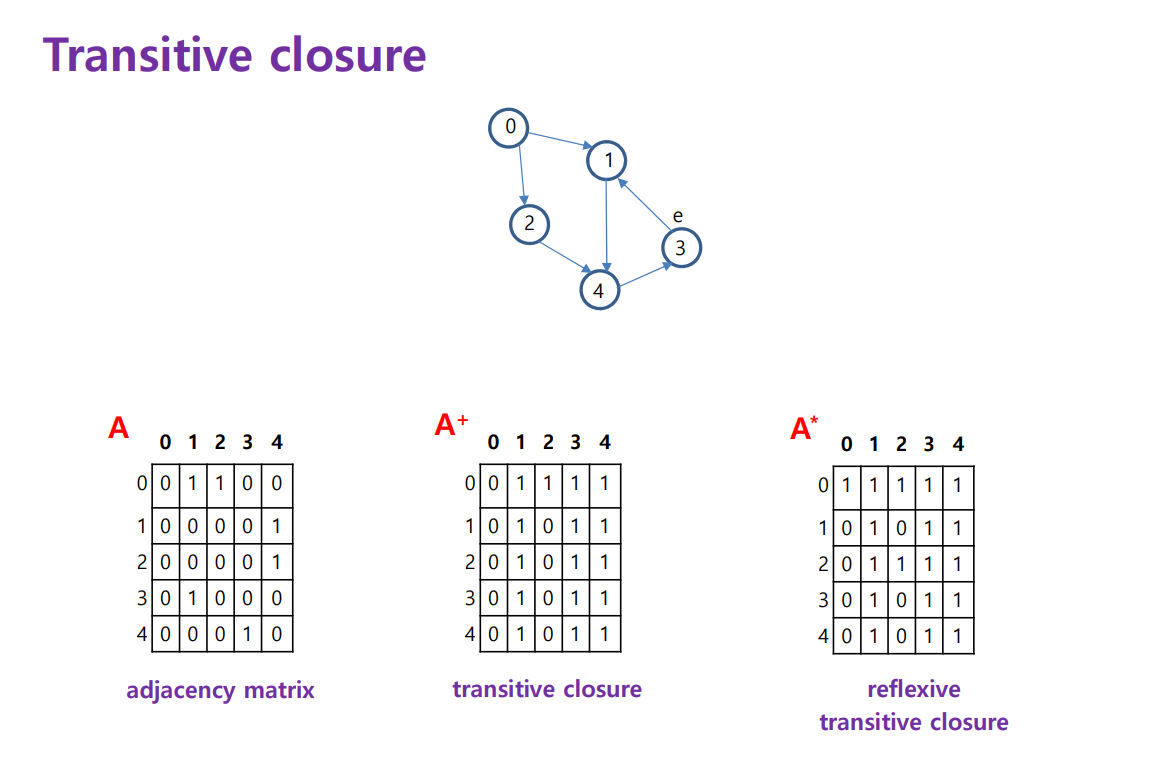
- Adjacency matrix = A --> vertex와 vertex간 EDGE가 존재하는가
- Transitive closure = A+ --> vertex와 vertex간 PATH가 존재하는가
\ 모양 대각선에 있는 1이 의미하는 바 : 자기에게 오는 path가 있다 = Cycle이다.
- Reflexive Transitive closure = A* --> vertex와 vertex간 PATH가 존재하는가 + 자기 자신 vertex에게 오는 path도 있다는 가정 = Transitive closured에서 \ 이렇게 대각선에 1이 존재함
그래프에서 vertex 에 대한 관계들
- Symmetric : 대칭적 ==> A --> B , B --> A
- Reflexive : 자신 ==> A --> A 인 관계
- Transitive : 전달 ==> A --> B , B --> C = A --> C
+ 셋 다 만족하는 건 Equivalent
A = 나 , B = 친구 라고 생각하면 편함.
Activity networks
Network = Edhe에 weight가 있는 거
AOV (Active on vertex network)
- A directed graph
- Vertex = 어떤 task or activity를 의미
- Edge = activity간 선후관계
ex) 교과 이수 과정

- Topological sort
--> Topological order를 찾기.
순서
1. predessor 가 없는 vertex 선택
2. 해당 vertex와 그 vertex의 outgoing edge를 삭제.
이거 하는 이유 : 다음 vertex의 predessor가 없는 생태로 만들어주기 위해 => 다음 vertex가 predessor가 됨

※ 모든 vertex가 선택되지 않는다면, cycle이 존재한다는 뜻.
출처 : 한동대학교 김호준교수님 - 데이터구조 ppt
'2학년 1학기 > 데이터 구조 ( Data structure )' 카테고리의 다른 글
| 데구 (0) | 2023.05.25 |
|---|---|
| 데이터 구조 15 ( graph AOE , Sorting ) (0) | 2023.05.21 |
| 데이터 구조 13 (0) | 2023.05.08 |
| 데이터 구조 12 (힙 추가 연산 , Binary Search Tree) (0) | 2023.05.01 |
| 데이터 구조 11 (Heap) (0) | 2023.04.24 |




