오래 못 할 짓 하지 않기
데이터 구조 18 (Huffman encoding , AVLtree) 본문
Huffman tree
two-way merge = 정렬된 2개의 리스트를 1개로 병합
ex) {1,3} {2,6} --> {1,2,3,6} merge sort라고 생각해도 될 듯
Hufffman tree는 이렇게 하나의 list를 만들 때, 최적의 순서를 찾는다.

이으려고 할 때, 작은 원소들을 먼저 결합시킨다
작은 원소의 후보는 두 개를 합쳐서 만들어진 원소도 후보가 될 수 있음.
예시로 [ 2 4 5 7 9 12 ] 이 원소들로 트리를 만들어보자.
우선 가장 작은 두 개를 먼저 결합 --> 2,4

이 떄 2,4를 6으로 바꿔줘도 될 것 같다.
리스트에 남은 원소는 [ 6 5 7 9 12 ]
가장 작은 6 5를 합쳐준다.

이런 형태가 되고 다시 리스트를 보면
[ 11 7 9 12 ] 가 된다.
여기에서 가장 작은 거 두 개 --> 7 9 임

리스트에 남은 건 [ 11 12 16 ]
작은 건 11 12

리스트에 남은 건 23 16
가장 작은 건 23 16

이렇게 가능함.
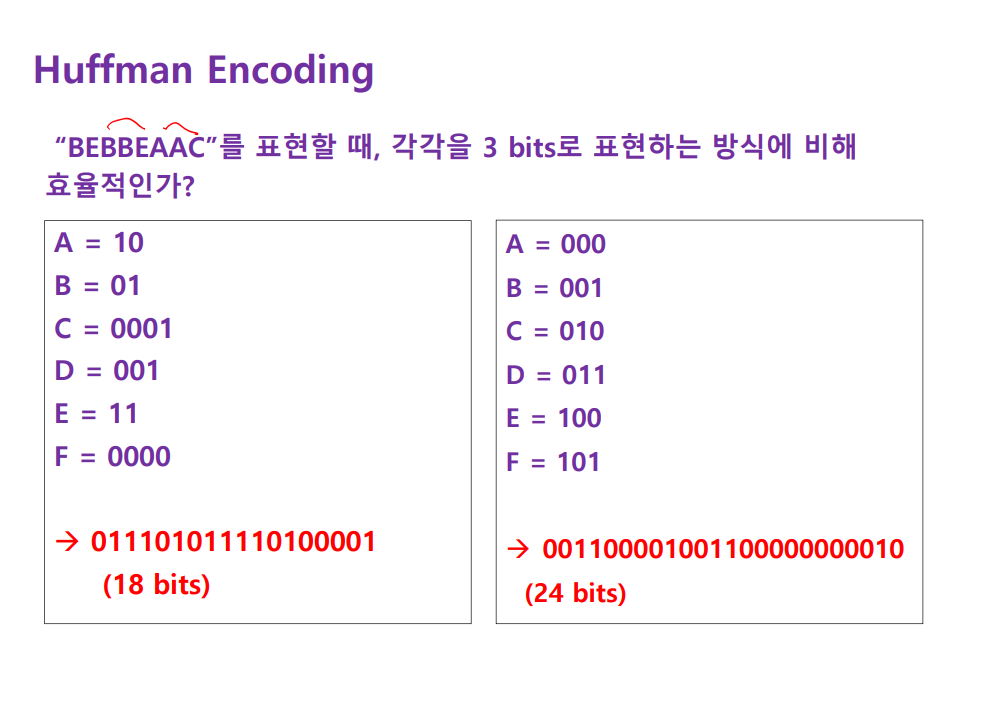
빈도수 개념을 넣어보자. 여기서부터 비트를 적게해서 메모리를 줄이는 것에 목적이 있다.

Tree의 왼쪽 branch를 취하면 0, 오른쪽은 1.
각 원소별로 몇 번씩 나오는지는 모르니 4개를 나타내기 위해 각 원소별로 2비트가 필요하다.
하지만 빈도가 알려졌다면??
많이 나오는 원소를 표현하는 비트를 적게하면 메모리를 많이 아낄 수 있지 않을까?

A의 빈도는 7, B는 12 이런 식으로 주어졌다고 생각해보자.
작은 (자주 안 나오는) 것은 밑으로 간다.
밑으로 가면 브랜치를 많이 거치기에 비트 수가 많아지긴하지만, 위에 있는 ( 자주 나오는 ) 것들은 비트 수가 줄어든다.
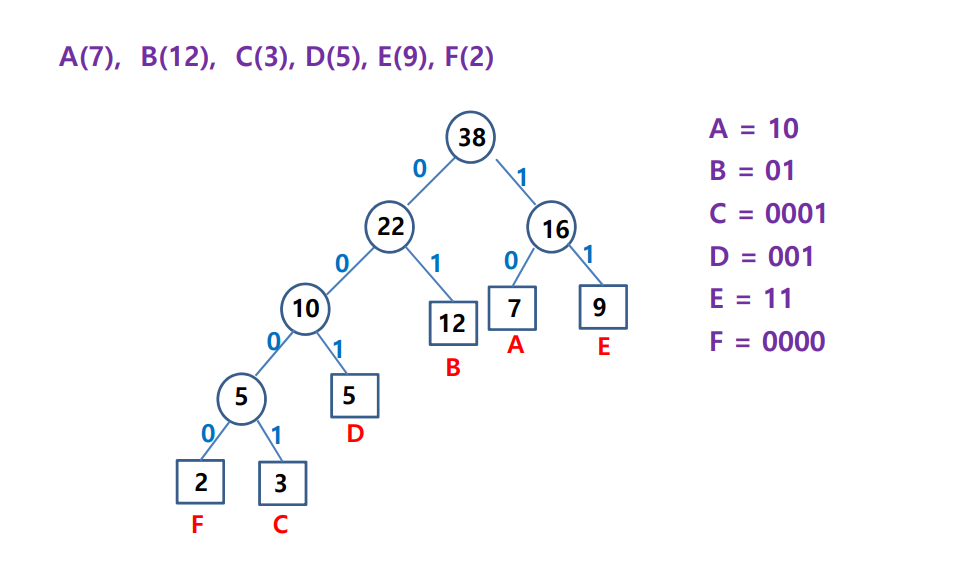
이렇게 나타낼 수 있다.
자주 안 나오는 애들한테 폭탄주고, 자주 나오는 애들한텐 꿀발라놓는다고 생각
AVL Tree
조건 1) BInary Tree의 형태여야 한다.
조건 2) Left subtree와 Right subtree 의 height의 차이가 1이거나 0이어야 한다.

분석 :
1) 20은 balanced 인가?
height of left sub = 3 / height of right sub = 3
두 개의 차이가 -1 ~ 1 범위 안에 들기에 [ balance ]
2) 27은?
height of left sub = 1 / height of right sub = 2
두 개의 차이가 -1 ~ 1 범위 안에 들기에 [ balance ]

Tree 연산


추가했을 때 tree가 imbalance 상태가 된다면 유형에 따라 4가지로 나눌 수 있다.

R R type --> 11이 balance가 맞지 않다.
왼쪽 0 , 오른쪽 2 = 차이 2 이므로 imbalance 상태이다.
오른쪽의 오른쪽이 길다는 뜻이니까
-->11기준으로 왼쪽으로 돌리면, 15가 올라간다.
그냥 imbalance인 거 3개 비교해서 중간에 있는 놈을 부모로 해서 오른쪽 왼쪽 으로 하나씩 놓는다고 생각하면 됨.
= height가 이전 상태에 비해 -1 (Binary tree 특징 이용)

LL type --> 11이 balance가 맞지 않다.
왼쪽 2 , 오른쪽 0 = 차이 2 이므로 imbalance 상태이다.
왼쪽의 왼쪽길어졌다는 뜻이니까.
-->11기준으로 오른쪽으로 돌리면, 5가 올라간다.
+ 15도 imbalance인데 왜 11을 고르냐? --> Minimal subtree를 고치기 때문에 11을 선택함.

LR type --> 15기준으로 balance가 맞지 않다.
왼쪽은 3, 오른쪽은 1이기 때문에 imbalance
[ Root : 15 / left subtree : 5 ]
1) Left subtree 기준으로 Left-Rotation
--> 5에서 Right가 더 길기때문에 left rotate를 하면 가운데 그림이 나온다
2) Root를 기준으로 Right-Rotation
--> 15에서 right rotate 하면 11이 위로 올라온다.
첫 번째 rotate를 했을 때 11이랑 9랑 노드로 이어져있었는데 떼짐.
부모노드가 위로 올라갈 때, 자식노드는 그 자리 지키면서 새로 그 자리에 온 부모의 자식이 됨...

RL type --> 5기준으로 balance가 맞지 않다.
왼쪽은 1, 오른쪽은 3이기 때문에 imbalance
[ Root : 5 / right subtree : 9 ]
1) right subtree 기준으로 right-Rotation
--> 9에서 left가 더 길기때문에 right rotate를 하면 가운데 그림이 나온다
2) Root를 기준으로 Right-Rotation
--> 5에서 right rotate 하면 7이 위로 올라온다.
다른 비유로 하면 싸움이 끝나면 진 사람이 내 짐을 가져가는 거임
7이랑 9랑 싸워서 7이 이기면 7의 짐(8)을 9가 가져가는 거임

분석:
20 --> left = 3 , right = 3 balance
27--> left = 0 , right = -2 imbalance
27 기준으로 RL Imbalance.
right subtree인 32 기준으로 Left rotate하고
root 인 27 기준으로 right rotate해준다.
옆으로 덤블링해서 상대방한테 간다고 생각해보셈
왼쪽으로 도는데 왼쪽 주머니에 있는 거 빠질까봐 먼저 간 애한테 주머니에 있는 거 맡기는 느낌.
왼족으로 돌면 왼쪽 거 맡기고
오른쪽으로 돌면 오른쪽 거 맡기고
(왼쪽으로 돈다는 건 상대방의 오른쪽에 내가 있다는 거니까 상대방 오른쪽으로 준다)

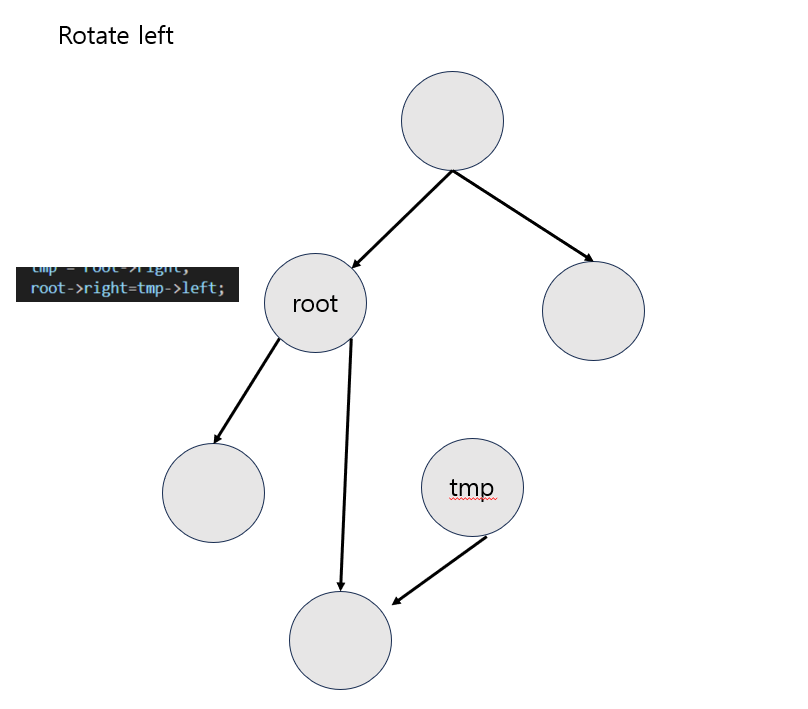
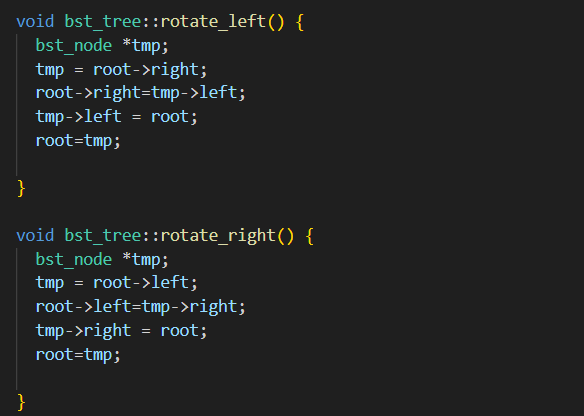
tmp = root->right root->right = temp->left
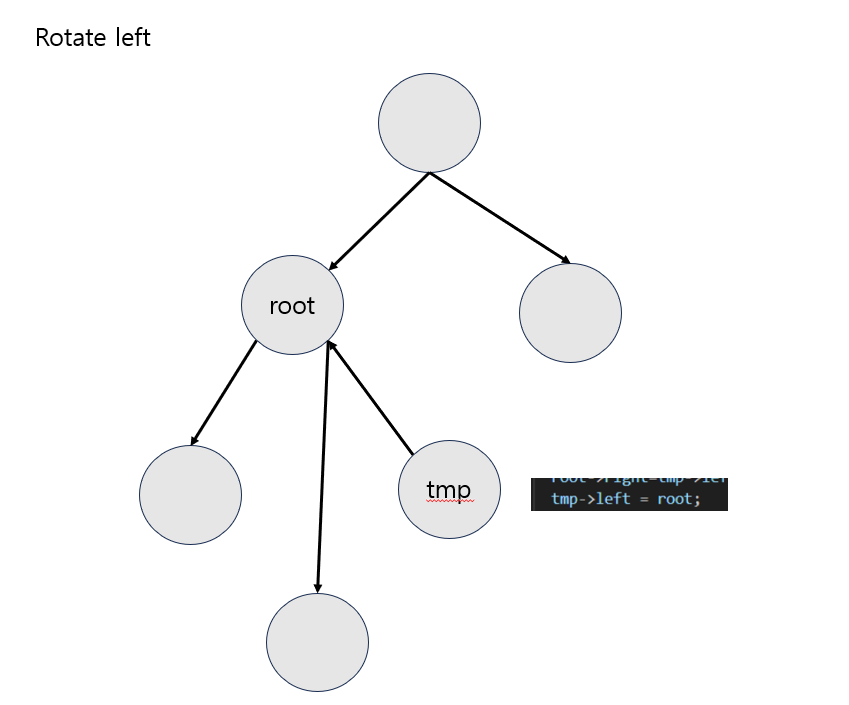

tmp ->left =root ; root =tmp
출처 : 한동대학교 김호준 교수님 - 데이터구조 PPT
'2학년 1학기 > 데이터 구조 ( Data structure )' 카테고리의 다른 글
| 데이터 구조 19 (0) | 2023.06.08 |
|---|---|
| 데이터 구조 기말 준비 (0) | 2023.06.05 |
| 데이터구조 17 ( Radix sort ) (0) | 2023.05.30 |
| 데이터 구조 16 ( Selection , Quick , Heap , Merge sort) (0) | 2023.05.26 |
| 데구 (0) | 2023.05.25 |




