오래 못 할 짓 하지 않기
[ 이산 수학 ] 6. 함수 본문
함수 : A와 B는 공집합이 아니면 A → B 이고
f: A → B라는 뜻은 A의 원소가 B 원소에 딱 하나에 할당된다는 것을 뜻한다.
따라서 원소 b가 f 함수에 의해 a원소에 의해 할당된 유일한 원소일 때 ' f(a)=b ' 이렇게 표현한다.
1) 두 원소는 하나의 쌍으로만 있어야 함수라고 할 수 있다

받는 건 겹쳐도 되는데 주는 놈이 2개를 보내면 안 됨
- 용어들
f: A → B 라고 할 때
1) f 는 A에서 B로 'maps'하거나 'mapping' 한다고 한다.
2) A는 f의 'Domain' , B는 f의 'Codomain'
3) f(a) = b 이면,
- b는 (f함수 아래 있는) a의 'image'이고
- a는 b의 'preimage'이다.
4) 함수 f의 범위 = 'images in A'이다.
따라서 f (A) = { f (x) | x E A }
5) 같은 Domain과 같은 Codomain을 갖고 있을 때
혹은 각각의 domain의 elements를 map했을 때, 같은 codomain 이 나오면
'두 개의 함수는 같다고 한다.'
Injection
일대일 함수 = One to one
: 각각의 Domain이 하나씩 Codomain을 가지고, 각 함수 결과값 (Codomain)은 고유하다.
특징
1) f(a) = f(b)이면, a=b 이다.
+ 대우로는 a!=b 이면 f(a) != f(b)이다.
→ 겹치면 안 된다 이말, 커플 매칭이랑 똑같다 보면 됨. 남자 1명 여자 1명

Surjection
전사 함수= Onto
(완전할 전, 쏠 사)
Injection 함수에서 한 조건이 빠진다.
' 1) f(a) = f(b)이면, a=b 이다. ' 이 조건이 없다.
따라서 그냥 Domain이 Codomain의 원소 중 하나만 찍기만 하면 성립함. 겹쳐도 ㄱㅊ
맞는 놈들도 다 맞아야 함 안 맞는 놈 있으면 X
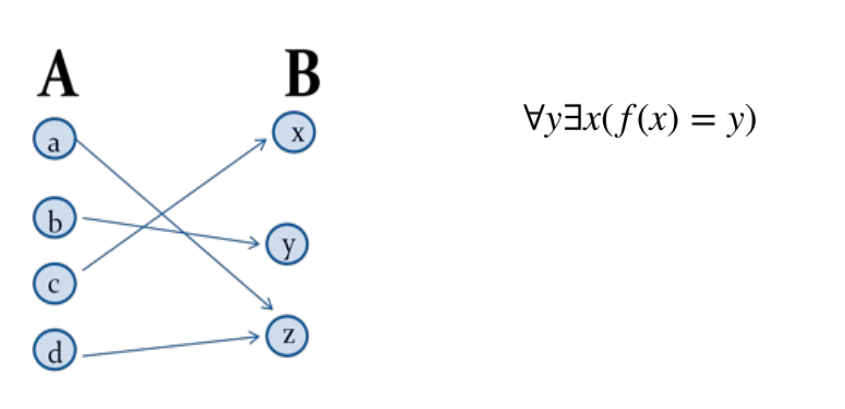
Bijection(Sur+Injective)
일대일 대응
: 다 쏴야하고, 받는 쪽도 다 겹치면 안 된다. + 안 맞는 놈도 없어야 한다.
Onto 함수와 One to One 함수 두 개를 만족하면 된다.
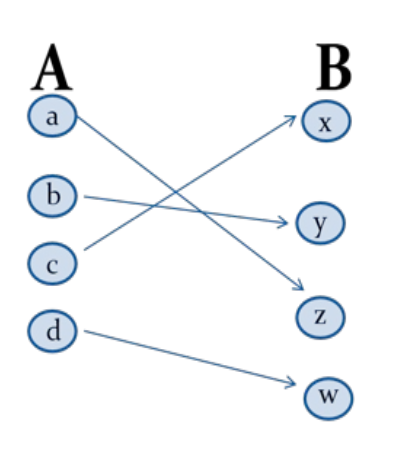
예시
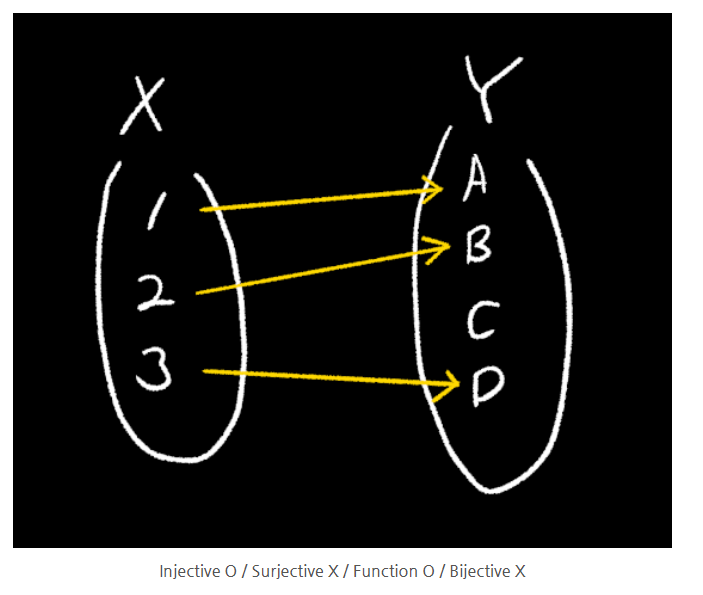
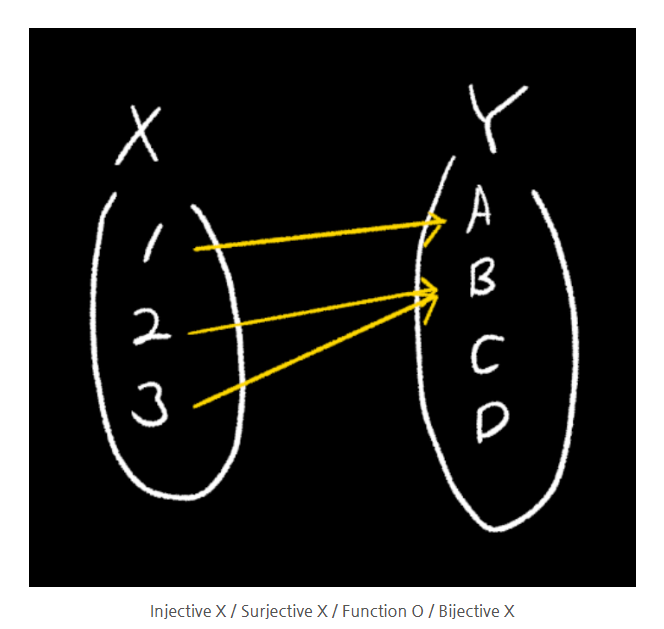
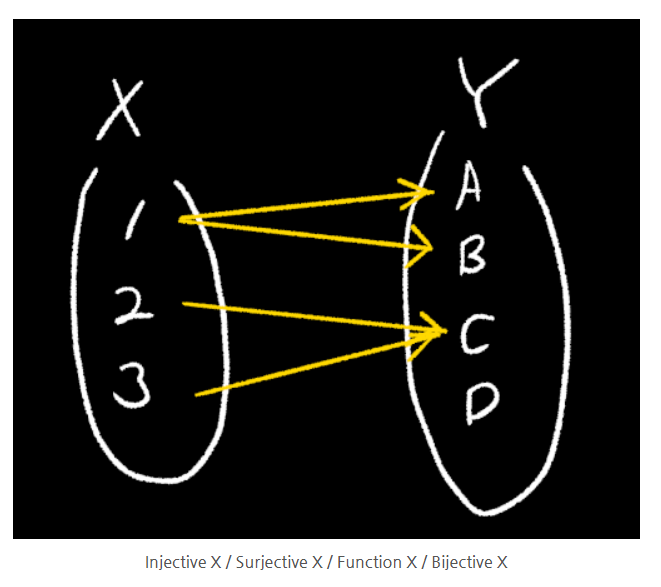
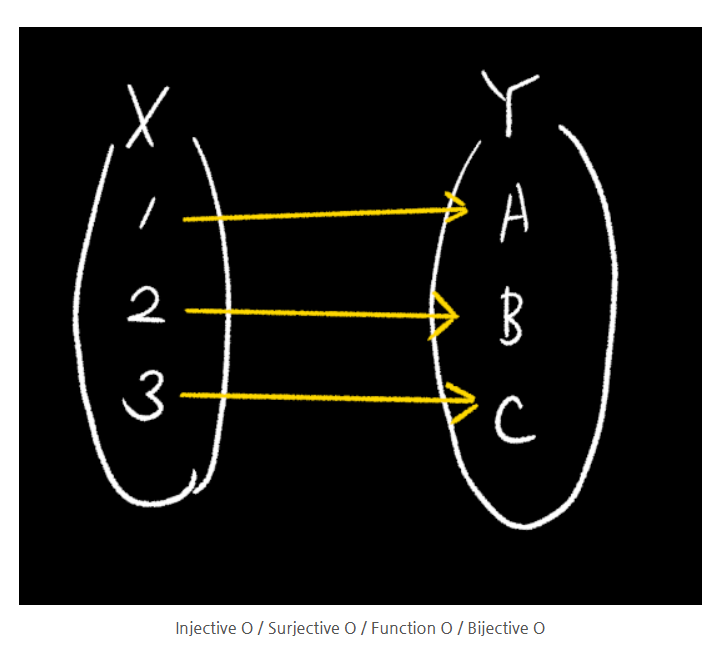
f : A → B 함수 판별법
● Injective인지 증명하는 법
: 만약 f(x) = f(y) 이고, x,y가 A의 원소이면, x = y 라는 것을 증명하면 됨
● Injective가 아닌 것을 증명하는 법
: 특정 원소 x,y가 A의 원소인데, f(x)=f(y)이면서 x!=y 인 것을 찾아라.
● Surjective인지 증명하는 법
: y가 B의 원소라 하고, f(x)=y로 만드는 A의 원소 x를 찾아라.
● Surjective가 아닌 것을 증명하는 법
: B의 특정 원소 y가 A의 모든 원소 x에 대해 f(x) !=y 로 만드는 것을 찾아라
= 안 맞는 놈이 있는지 봐라
Inverse Functions
역함수
: 함수 f가 A → B에 일대일대응일 때
역함수 f'는 B →에 대한 함수이다.
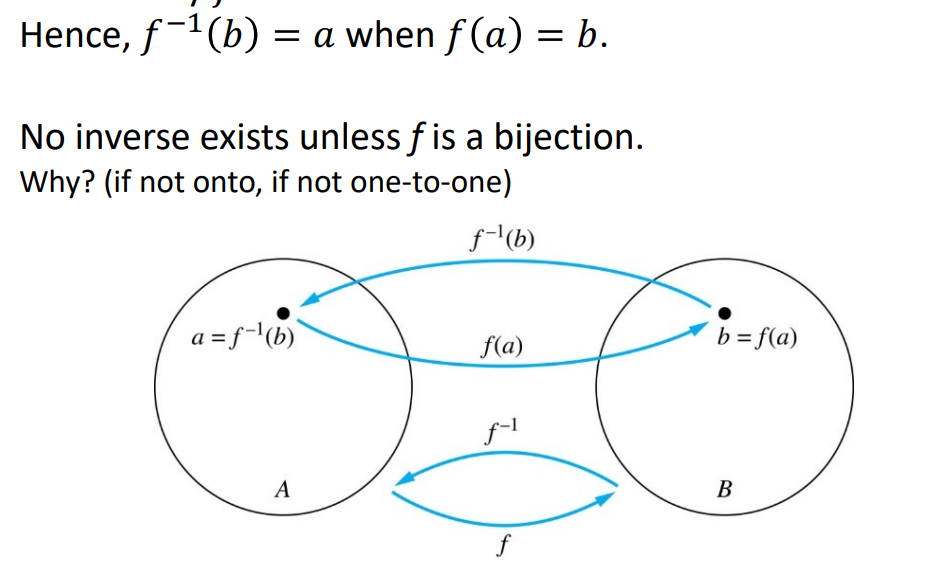
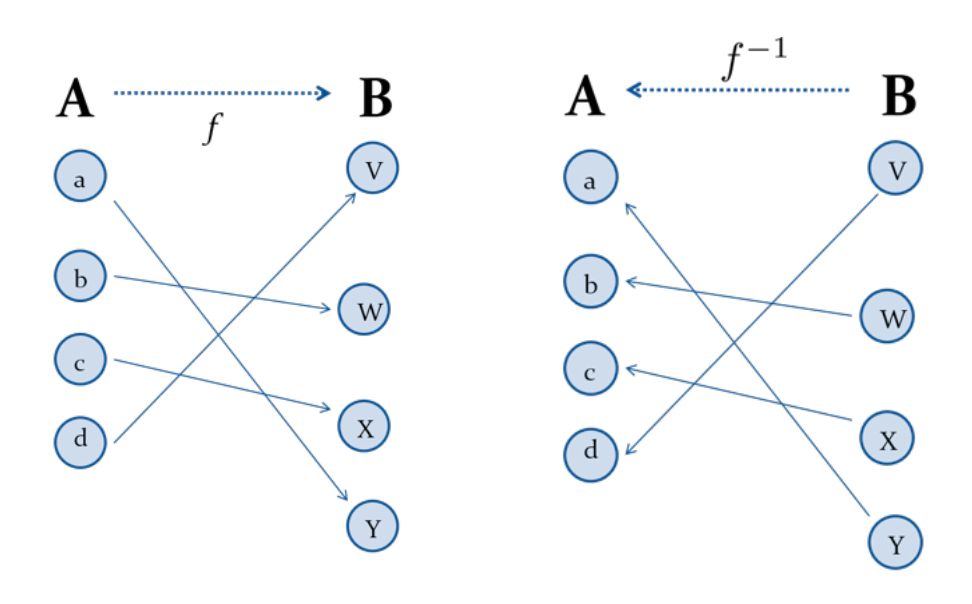
Composition
한국말로 뭐라했는지 까먹음
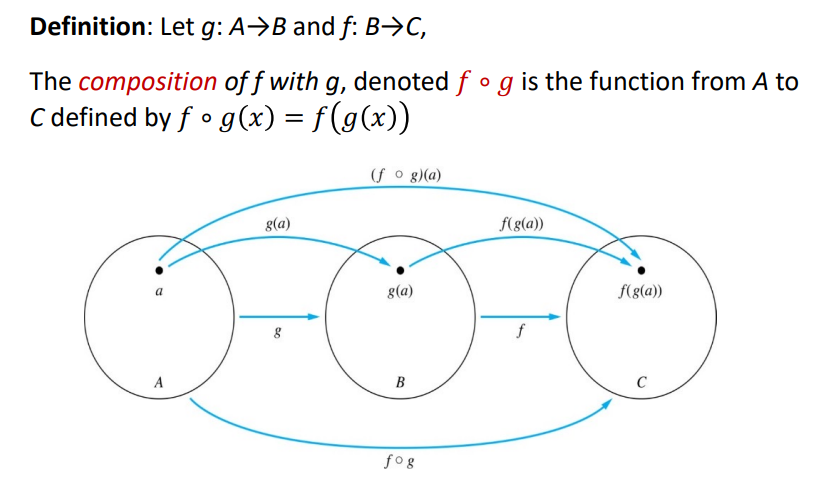
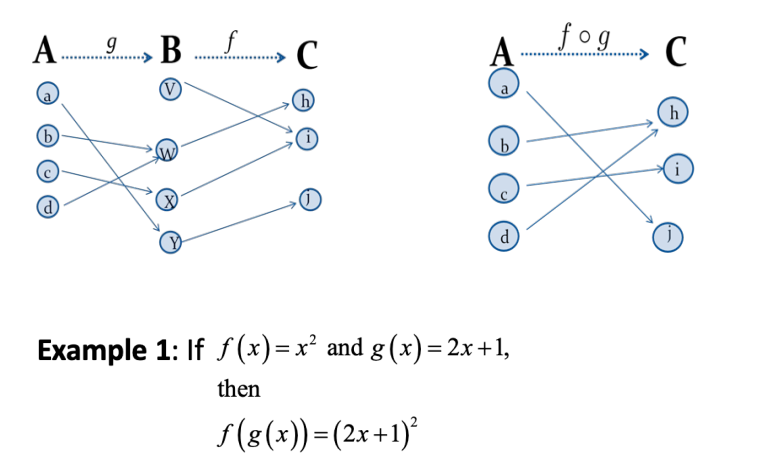
순서 중요하다 이 정도만 알면 될 듯
그래프 함수
함수에 대해서 선이 아니라 그냥 점 찍어서 그래프 만드는 거
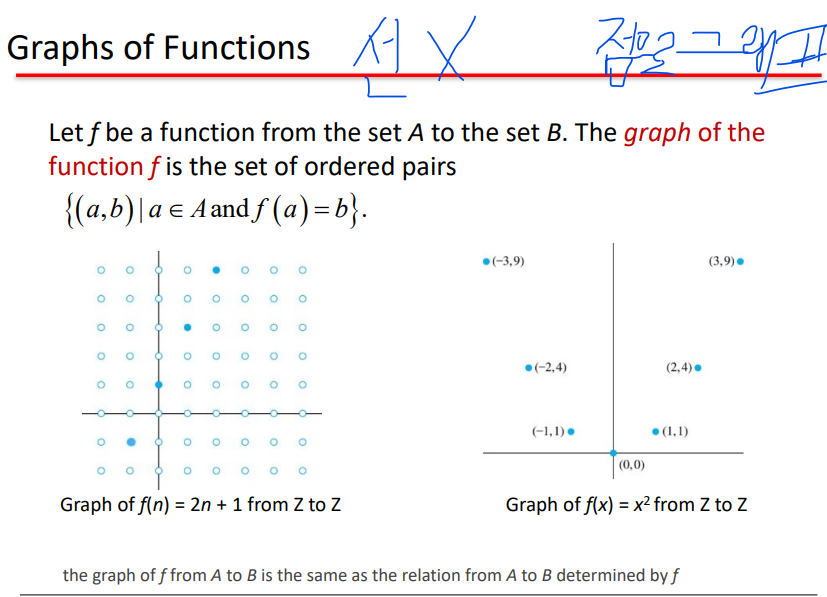
Floor / Ceiling
- Floor
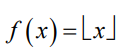
밑에 씌우면 반내림
이렇게 생겨서 밑이 막혀있는 구조이다. 그냥 밑에 안 막혀있고 저 부분으로 빨려간다고 생각하면 된다.
아래가 뚫려있으니 숫자 소수점이든 뭐든 아래로 간다고 생각하면 됨.
- Ceiling
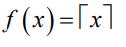
위에 씌우면 반올림
위에 구멍으로 빨려 올라간다고 생각하면 된다.
**** 음수에서 조심해야함!! 실수하기 쉬움 ****

따라서, 이런 문제 풀 때 이렇게 그려서 하기
수열
- 등차수열
- 등비수열
위에 두 개도 설명했는데 어차피 고등학교 때 마스터하고 와서 넘어감
- 점화식
일부 점화식 특징 ) 초기값 안 주면 시작 못 함

그런 점에서 피보나치 이런 게 잘 되어있음
1) 초기값 제시
2) 규칙 설명
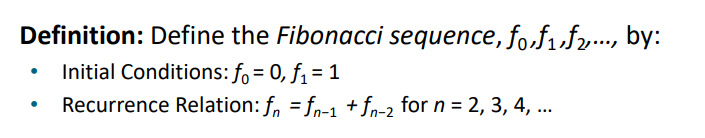
Iterative Solution
반복 해법
1) Working upward
: 주어진 초기값이나 조건을 가지고 다음 n=1,2,3,4 ... 전개해보면서 규칙을 찾는 방법

2) Working downward
: upward와 반대로, n에서부터 시작하여 n= n,n-1,n-2...3,2,1 이렇게 내려가서
n과 초기값으로 정리되는 식을 구하는 방법

수열의 합
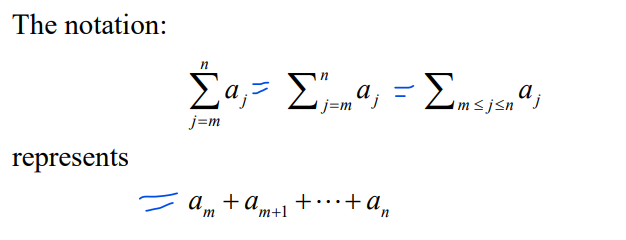
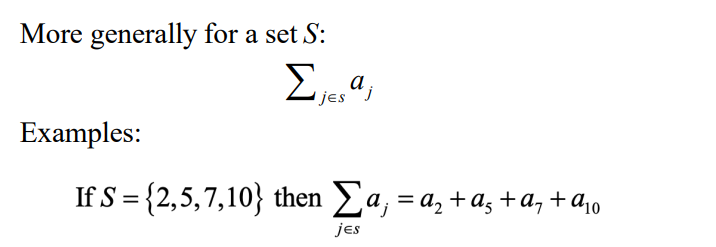
수열의
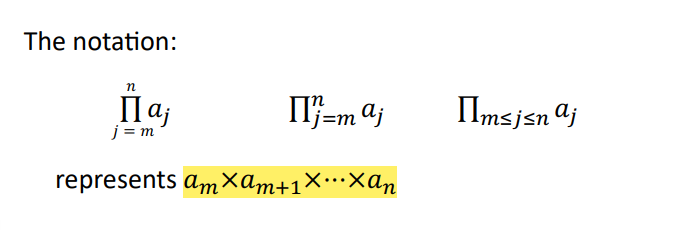
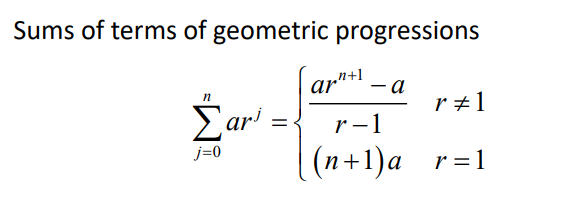
(출처)
한동대학교 최희열교수님 - 이산수학
https://blog.naver.com/sw4r/222615061545
https://blog.naver.com/PostView.naver?blogId=obrigadu&logNo=50100112933
'2학년 2학기 > 이산수학' 카테고리의 다른 글
| [ 이산 수학 ] 8. 수학적 귀납 (0) | 2023.09.26 |
|---|---|
| [ 이산 수학 ] 7. Cardinality , 행렬 (0) | 2023.09.18 |
| [ 이산 수학 ] 5. 집합 (고등학교 내용과 비슷함) (0) | 2023.09.12 |
| [ 이산 수학 ] 4. premises ( 전제 ) (0) | 2023.09.08 |
| 이산 수학 3 (0) | 2023.09.04 |




