오래 못 할 짓 하지 않기
[ 알고리즘 ] 10. Knapsack 본문
Knapsack problem
( 배낭 알고리즘)
한 도둑이 박물관에 쳐들어가서 물건을 훔친다.
가져갈 수 있는 배낭의 크기는 정해져 있으므로
어떻게 훔쳐야 가장 이득(?)일까? 를 고려하는 알고리즘이다.
케이스는 두 가지로 나뉜다.
1) 0-1 knapsack
: 조각상이나 모나리자 같은 작품은 가져오거나 안 가져오는 거임. 쪼개거나 부수면 가치가 사라진다.
= 담으려는 Item을 쪼갤 수 없는 경우
이런 경우에는 DP로만 해결할 수 있으며
Greedy 알고리즘은 효과가 없다.
2) Fractional kanpsack
: 다이아가루, 금가루는 그냥 쪼개서 들고 나와도 괜찮음
= 담는 Item을 쪼갤 수 있는 경우
이 때는 반대로 Greedy 알고리즘만 사용할 수 있다.
1. Fractional knapsack problem
이 알고리즘은 생각보다 간단하다.
가방에 10만큼 넣을 수 있으면 싼 거를 채우는 게 아니라,
시작 : 가장 비싼 거 먼저 다 담기
▶ 남은 공간이 있다면 그 다음 비싼 거
▶ ...
이렇게 진행하면 된다.

근데 우린 주로 이걸 안 씀
왜냐면 정수로 계산을 하기 때문에 쪼개는 게 좀 애매함 ㅋㅋ
2. brute force approach
그냥 하나하나 다 가방에 넣어보면서 되네 안 되네 이러면서 해보는 거
- n개의 Item이 있을 때, 2^n의 경우의 수가 있다. ( 논리설계 경우의 수 생각하면 됨 )
- Θ(2^n)

3. Dynamic Programming

Q : 총 n개의 아이템이 있을 때, Sn 에 대한 solution은 Subproblem Sk 로 해결 가능한가?
A : ㄴㄴ

S5의 Solution은 Optimal Solution인 S4를 통해 풀 수 있어야 하는데
그게 아님.
S5의 Solution에는 S4의 Solution이 포함되어야 하는데 없다.
따라서, 우리는 Subproblem 을 다시 설정해야 한다.

이를 그림으로 보면 다음과 같다.
B[ K , W ]
Case 1 ) wk 가 W 보다 더 커서 들어갈 수 없을 땐, 그냥 B[ K-1 , W ] 를 사용한다.
Case 2 ) [ Wk가 들어갈 자리가 없는 경우 ] [ B[ K-1 , W-wk ] + bk ] 이 둘 중에 더 큰 값을 가져간다.


두 번재 케이스에 대해...▼

▼ Knapsack DP 알고리즘 Pseudocode

4. Branch and Bound
: 트리 형태로 Item들을 나누고, 갈만한지 아닌지를 판단해서 Expand하는 형태이다.

각각의 노드가 가지고 있어야 하는 값들은 다음 3개와 같다.
- Benefit : 해당 노드까지 포함해서 얻게 되는 총 Value
- Weight : 해당 노드까지 포함해서 쌓인 총 Weight 값
- Bound : 이 노드를 넘어서 계속 확장했을 때 얻게 될 수 있는 Benefit의 Upper bound
이들은 각각의 노드에 저장되어 있다. = Local values

bound 는 W 를 넘지 않는 선에서 node(item)들을 더해서 얻는 값들을 말한다.

총 Weight 100까지만 담을 수 있는데 80이 차있다.
= Weight 를 20만 더 채울 수 있음
> 새로 들어오려고 하는 건 40임
> 얘를 남은 크기에 맞춰 나눈다. = ( 100 - 80 ) * ( 30 / 40 )
= 지금껏 얻은 Value + 남은 크기에 맞게 넣었을 때 얻는 Value
= 150 + 15 = 165


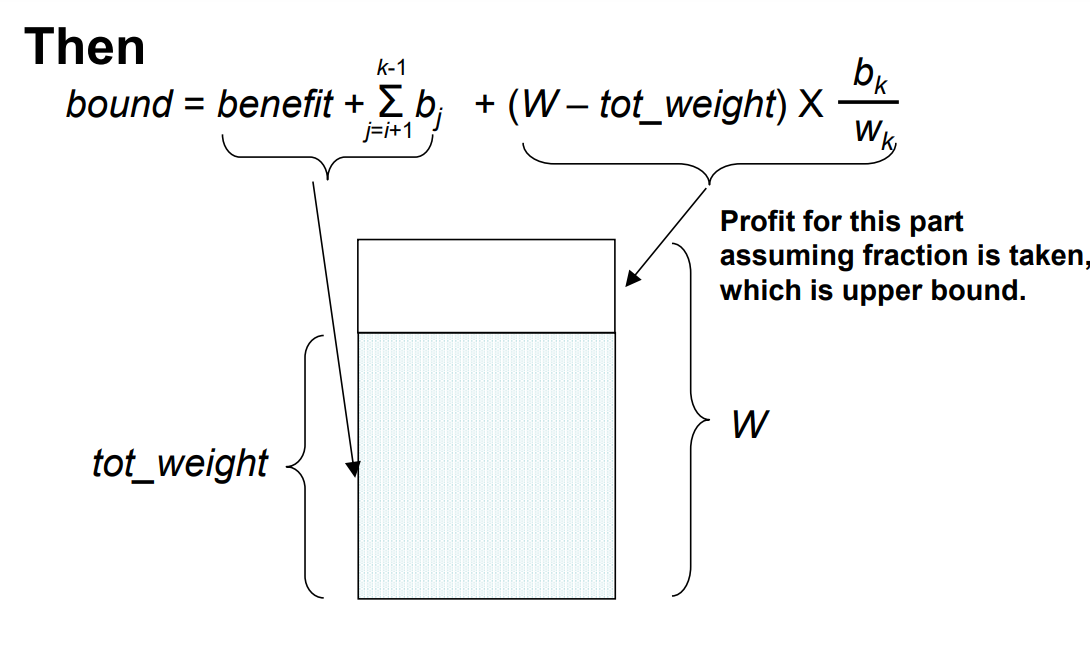
Bound = ( 지금까지 얻은 Benefit ) + { ( 남은 크기 ) * 쪼개서 넣으면 얻을 수 있는 value }
추가로 우리는 max_benefit에 대해서는 Global value로 항상 참조해야한다.
(처음엔 0으로 초기화)
max benefit 업데이트는
현재까지 업데이트 된 [ Max_benefit , 현재 노드가 가지고 있는 총 benefit ] 중에 큰 값으로 한다.


Bound 와 Max_benefit의 차이
● Bound - 현재 노드에서 더 뻗어 나갔을 때 얻을 수 있는 Benefit의 Upper bound(상한선, 최댓값)
● Max_Benefit - 지금까지 나온 Best Solution의 Benefit
● Promising / Non - promising
노드가 Expand를 하는데 어떤 걸 기준으로 Expand할지 말지를 판단해야할까?
▶ Promising / Non - promising 으로 판단한다.
- Promising - 이 노드를 기준으로 Expand로 한다.

여기로 계속 갔을 때 얻는 bound가
현재 등록되어있는 max_benefit ( best solution의 benefit ) 보다 더 크다.
- Non - Promising - 이 노드를 기준으로 멈춘다.

여기로 계속 갔을 때 얻는 bound가
현재 등록되어있는 max_benefit ( best solution의 benefit ) 이하임.
= 계속 가봤자 현재 등록된 애보다 나은 게 없다.
OR
지금 넣으려고 하는 node의 Weight가
담을 수 있는 크기보다 크면 Non promising

사용 예제
1) BFS 적용
2) Primising인데 Expand되지 않은 Greatest bound를 가진 node를 고른다.
+ Node들은 무게당 value (= bi / wi ) 가 높은 순서대로 정렬시켜놓는다.

4개의 item / 넣을 수 있는 총 Weight = 16
0 번 Vertex : 아무것도 넣지 않은 상태 ▶ max_benefit : 0
- Benefit : 0
- Weight : 0
- total_Weight : 현재 weigth + 앞으로 자르지 않고 넣을 수 있는 거 ( order대로 )
= 0 + (2+5) = 7 <W
= (아직 넣진 않았는데 이따 넣으면 안 쪼개고 넣을 수 있는 것들)
- Bound : 0 + ( 40 + 30 ) + 45 = 115 > max_benefit
→ 이 방향으로 expand
(1,1)번 Vertex : 1번 Item을 넣은 상태 ▶ max_benefit : 0
- Benefit (지금까지 총합) : 40
- Weight : 2
- Max_benefit : max( 원래 값 , 지금 값 ) = max( 0, 40 ) = 40
- total_Weight : 2 + (5) = 7
- Bound : 0 + 40 (+ 30 ) (+ 45) = 115 > max_benefit
→ 이 방향으로 expand

(2,1)번 Vertex : 2번 Item을 넣은 상태 ▶ max_benefit :40
- Benefit (지금까지 총합) : 70
- Weight : 7 < W
- Max_benefit : max( 원래 값 , 지금 값 ) = max( 40 , 70 ) = 70
- total_Weight : 2 + 5 = 7 < W
- Bound : 0 + 40 (+ 30 ) (+ 45) = 115 > max_benefit
→ 이 방향으로 expand
(2,2)번 Vertex : 2번 Item을 선택하지 않은 상태 ▶ max_benefit :70
- Benefit (지금까지 총합) : 40
- Weight : 2 < W
- Max_benefit : max( 원래 값 , 지금 값 ) = max( 40 , 40 ) = 40
- total_Weight : 2 (+ 10) = 12 < W
- Bound : 0 + 40 (+ 50) +(8) 98 > max_benefit
→ 이 방향으로는 갈 수는 있는데 위에 있는 Bound가 더 크므로, (2,1) 노드부터 Expand한다.

(3,1)번 Vertex : 3번 Item을 넣은 상태 ▶ max_benefit :70
- Benefit (지금까지 총합) : 120
- Weight : 7 + 10 = 17 > W
→ 이 방향으로 expand 못 함
(3,2)번 Vertex : 3번 Item을 선택하지 않은 상태 ▶ max_benefit :70
- Benefit (지금까지 총합) : 70 +0 = 70
- Weight : 7 < W
- Max_benefit : max( 원래 값 , 지금 값 ) = max( 70 , 70 ) = 70
- total_Weight : 7 (+ 5) = 12 < W
- Bound : 40 + 30 + 10 + (하고도 공간이 남음) = 80 = > max_benefit
→ 이 방향으로 expand 가능은 함 Promising임
근데 우리가 계속 가고 있었던 Promising Node를 보고 Bound가 가장 큰 (2,2)를 다시 Expand한다.
(3,2)번 Vertex : 3번 Item을 선택한 상태 ▶ max_benefit :70
- Benefit (지금까지 총합) : 40 + 0 + 50 = 90
- Weight : 2 + 0 + 10 < W
- Max_benefit : max( 원래 값 , 지금 값 ) = max( 70 , 90 ) = 90
- total_Weight : 2 + 0 + 10 = 12 < W
- Bound : 40+ 0 + 50 + (4번 item을 남은 공간에 잘라넣음)( = 9 ) = 98 > max_benefit
→ expand 한다.
max_benefit :90 으로 업데이트

더 못 감
이거 연습 더 해봐야 할 듯
(출처)
한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 12. DFS (0) | 2024.04.28 |
|---|---|
| [ 알고리즘 ] 11. BFS (0) | 2024.04.26 |
| [ 알고리즘 ] 9. DP / Greedy 문제 풀기 (0) | 2024.04.13 |
| [ 알고리즘 ] 8. Huffman 알고리즘 (0) | 2024.04.07 |
| [ 알고리즘 ] 7. Greedy 알고리즘 (2) (0) | 2024.04.07 |




