오래 못 할 짓 하지 않기
[ 알고리즘 ] 11. BFS 본문
Graph Traversal
: Graph G에 있는 모든 Vertex를 방문하는 것이다.
● 모든 Vertex를
● 한 번만
방문하는 알고리즘 2가지
1) BFS ( Breadth First Search ) - QUEUE 로 구현
2) DFS ( Depth First Search ) - STACK으로 구현
BFS ( Breadth First Search )
(Tree 형태 기준) Level Order 방식
Root 로 설정한 노드에서 연결되어있는 노드들을 Discover 하고 , 그 사이에 있는 Edge를 Explore 했다고 할 수 있다.
+ Discover and Explore의 기준은 목적지에 있는 노드가 Discover 되지 않았을 때

1. Root 노드인 A → 연결되어있는 B,C 를 (알파벳)순서대로 Discover , 그 사이에 있는 Edge들을 Explore
2. B가 연결되어있는 D 를 Discover , 그 사이에 있는 Edge를 Explore.
모든 Vertex 들어가기 완료
+ B,C는 연결되어있지만 둘 다 Discovered 상태이므로 그 사이에 있는 Edge는 Explore되지 않는다.
이번 챕터에서는 Vertex의 색으로 구분을 한다.
● White = Dicover 되지 않은 Vertex
= 모든 Vertex의 기본값
● Gray = Discover는 되었지만 탐사하지 않은 Vertex
+ White vertex와 인접해있음 + (인접 and White) 였던 애들이 Black으로 되면 같이 Black으로 됨
● Black = Dicover 되고 Child가 없으면 (= 끝났으면 ) 바뀐다.
= 아래로는 Black , 위로는 Gray와 인접할 것이다.
BFS 알고리즘
1. White Vertex를 Dicover 했다.
▶ 해당 Vertex를 Gray로 바꾼다.
▶ 인접한 White Vertex를 Discover한다.
2. 인접한 모든 Vertex를 Discover 했다면
▶ 자기 자신을 Black으로 바꾼다.

분석

코드를 2부분으로 나눠서 보면
● For 부분 : 초기화
> Src vertex만 Gray, 나머지는 White
> 모든 Distance = 무한대
> 모든 vertex는 자신의 부모 노드가 없다는 걸 설정함.
= 부모 자식관계가 아니라 인접한 관계로 만들어둠.
● While 부분 : Traversal
> Q에 있는 거 하나 꺼냄 = u
> u 에 인접한 vertex들로 반복문을 돌린다.
>White vertex면 Gray로 바꿈
> 해당 vertex의 Distance = d[u] +1
> 해당 vertex의 부모 = u
> 해당 vertex 를 Queue에 넣음
반복이 끝나면 = 인접한 거 다 봤으면 u = Black

예제

BFS문제를 풀 때는
Vertex는 섬
Edge는 다리 라고 생각하면 이해가 쉽다.
Root 섬에서 사람'들'이 동시에 한 다리씩 건너면서 이동한다. ( 각자 가고싶은, 갈 수 있는 곳으로 감 )
초기화 단계

1번 실행
인접한 노드 방문 후 - > 거리 1추가 + 회색으로 변경
S는 인접한 게 없으므로 Black으로 변경


이 흐름으로 계속 가면 된다.
▼
2번 실행


3번 실행

4번 실행
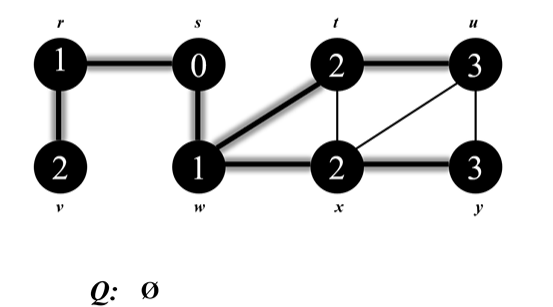
결론적으로 x-u , y-u 다리는 건너지 않는다.
최종 Search 후 vertex에 있는 Distance들과 Edge를 고려해서 Tree로 만들 수 있다.

예제 2

풀어보기▼
(출처)
한동대학교 용환기 교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 13. DFS - 활용 (0) | 2024.04.29 |
|---|---|
| [ 알고리즘 ] 12. DFS (0) | 2024.04.28 |
| [ 알고리즘 ] 10. Knapsack (0) | 2024.04.13 |
| [ 알고리즘 ] 9. DP / Greedy 문제 풀기 (0) | 2024.04.13 |
| [ 알고리즘 ] 8. Huffman 알고리즘 (0) | 2024.04.07 |






