오래 못 할 짓 하지 않기
[ 알고리즘 ] 23. Medians and Order statistics 본문
Median = 중간값
ith Order static = i 번째로 작은 값
ex) Minimum = 1st order statistic
Maximum = nth order statistic
Median = 홀수면 (n+1) /2 , 짝수면 n/2
가볍게 생각해보기 좋은 것
: n개의 숫자에 min과 max찾기
> 'min과 max를 찾으려면 각각 n-1번 비교'
총 2n-2
'n-1번만 해서 두 개를' 구할 순 없을까?
n이 짝수일 때, 한 쌍을 잡아두고, 거기에서 큰 걸 Max으로, 작은 걸 Min으로 해서
두 쌍 중에 Min set와 Max set을 만든다.
ex) 가위바위보 진 팀 , 이긴 팀
이렇게 나눈다면 각각의 set은 (n-2) / 2 가 되고,
그 안에서 각각 min과 max를 찾으면 된다.
The Selection Problem
i 번째 작은 element를 찾는 문제
● Worst case
: Sorting 후 i번째 index 값을 가져온다

이거보다 좀 더 짧은 알고리즘은 없을까
1. Randomized Algorith
: Quicksort에서 하던 Partition()을 사용한다.
i) 찾으려고 하는 값이 pivot보다 작으면 작은 쪽 subarray만 본다.
그 sub array에서 i번째 값을 찾는다.
ii) Pivot보다 크다면? i-k번째 값을 pivot보다 큰 subarray에서 찾는다.
= subarray가 하나만 필요함!
i : 우리가 찾으려고 하는 숫자
k = pivot

= Average case 에서 세타 (n)

A = array
p = 시작 index
r = index
i = 찾는 i th smallest 값
1번째 줄 : array크기가 1일 때 바로 return
2번째 줄 : partition 해서 pivot의 index return
3번째 줄 : 크기가 8일 때, 3번째로 큰 애를 찾으려면, 3-1+1 =3
pivot보다 큰 경우에 7번째 큰 애를 찾는다면, 7-5+1 =3
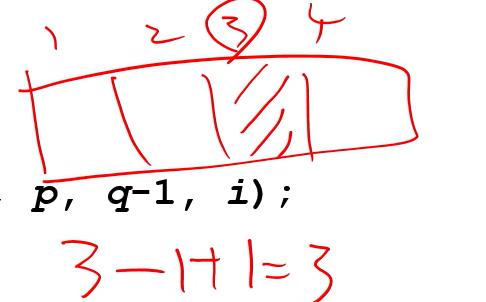
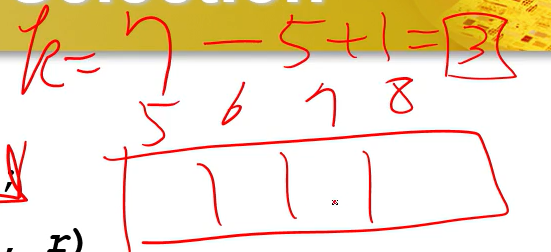
이거 다른 곳에서 더 찾아보기

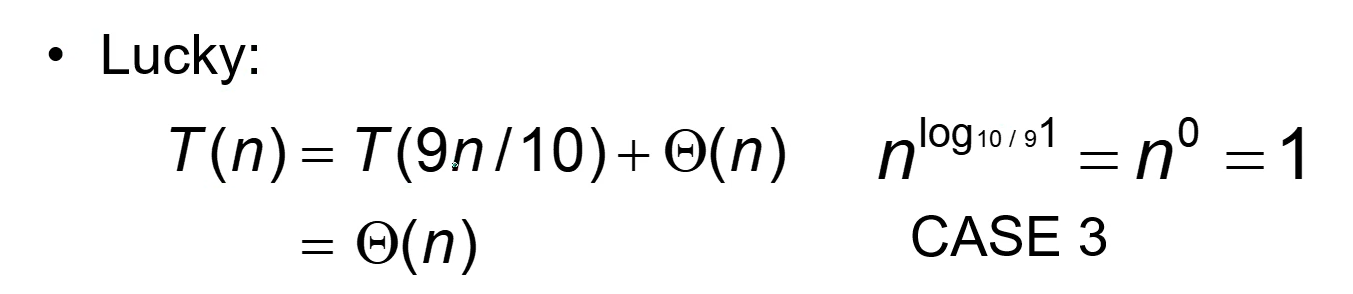
그나마 worst case가 아닐 때, 즉 2개의 subArray로 나뉠때,
99:1이어도 되니까 2개로 나뉠 때는 세타(n)의 time complexity를 가진다.

하지만 고르는 것이 계속 가장 작은 element일 때는 세타(n^2)이 나온다.

k = pivot (Paritition)
근데 같은 숫자들이 2번씩 나오니까
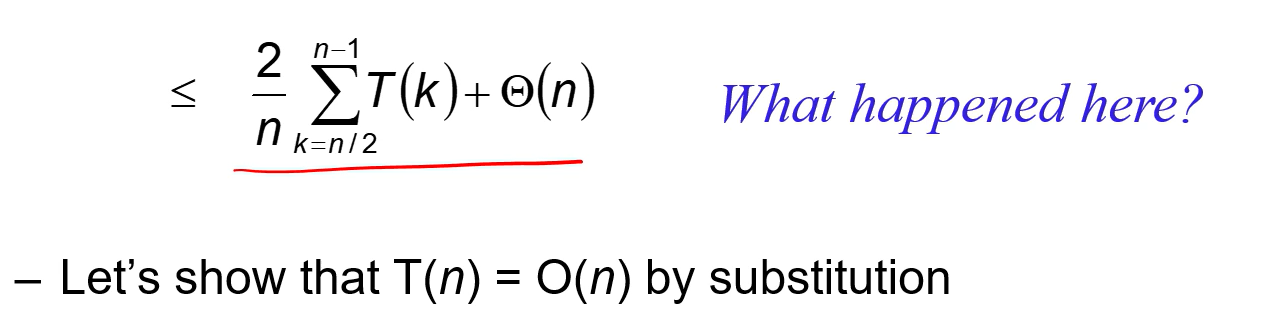
너무 복잡해서 안 봐도 된다고 하심
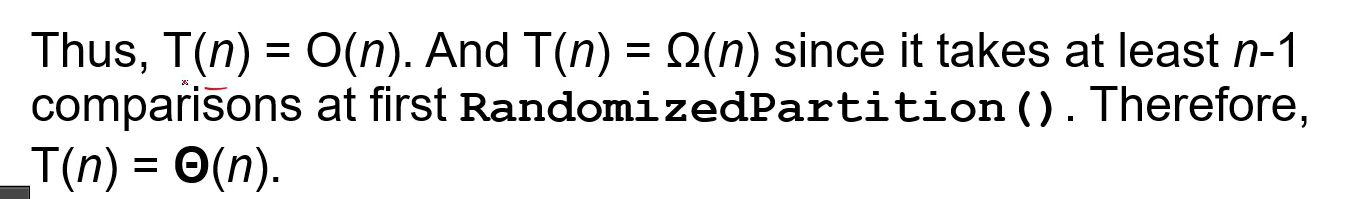
2. (이론적으로) Cool Algorithm
= Worst case 에서 세타 (n)

1~3 : Worst case가 생기지 않을 좋은 Pivot을 찾는다.
4 : pivot x를 기준으로 partitioning한다.
5~ : Quick sort와 같다.
예제)

1. 5개의 그룹으로 나눈다.

2. 각각의 그룹에서 Median을 찾는다.
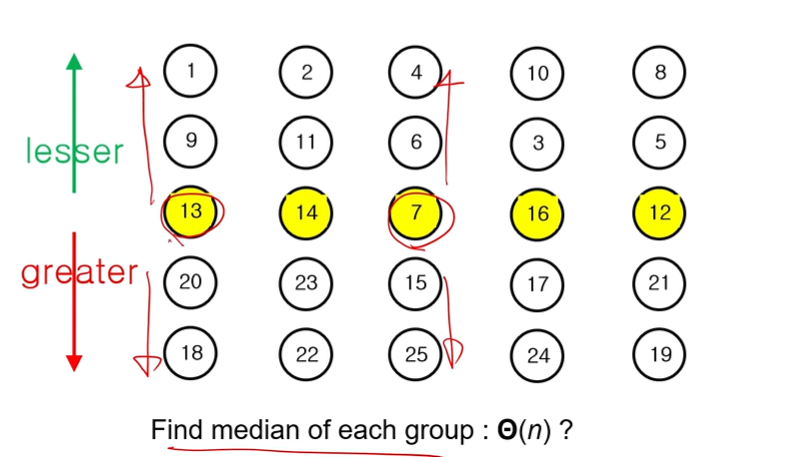

3. Median들 중의 Median을 찾는다. = 13
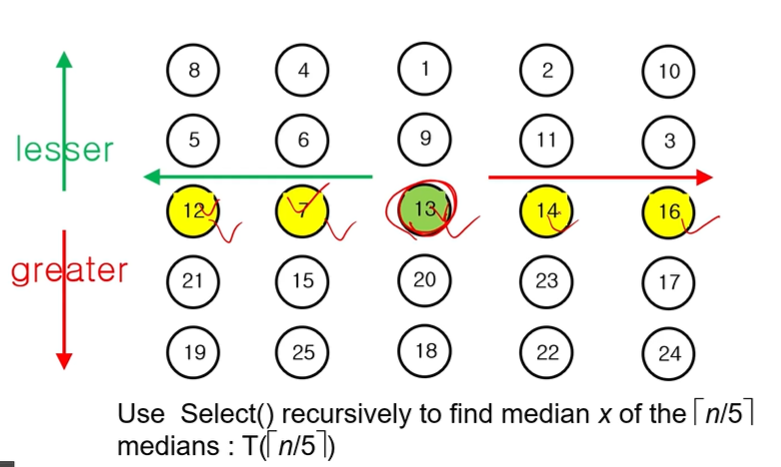
4. Median의 Median이므로, 최소 얘보다 작은 애가 3 [ n/10 ] 개는 존재한다.
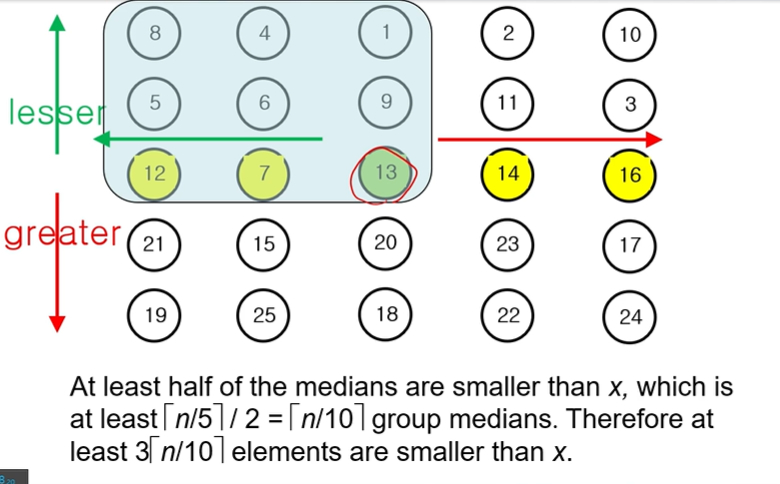
+
Median의 Median이므로, 최소 얘보다 큰 애가 3 [ n/10 ] 개는 존재한다.
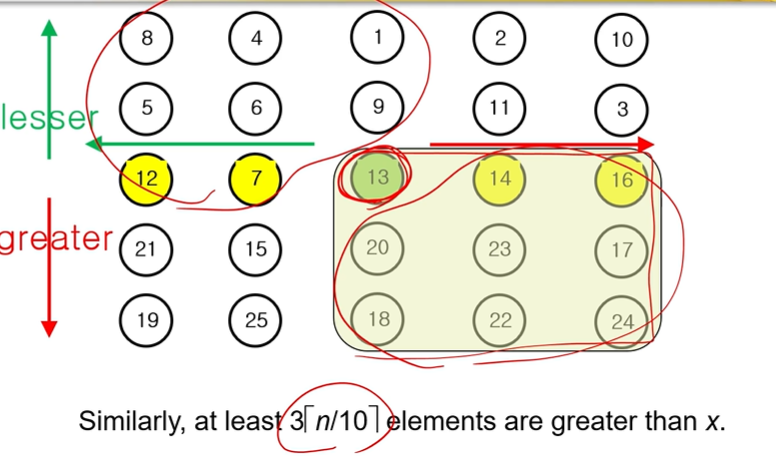
1,3사분면 element만 검사하면 될 것이다.
5. 나머지 애들을 Pivot과 비교하면서 Sort한다.
= 세타( 4n/10 ) = 세타(n)


(출처)
한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 25. String matching 2 - KMP (0) | 2024.06.11 |
|---|---|
| [ 알고리즘 ] 24. String match (0) | 2024.06.10 |
| [ 알고리즘 ] 22. Counting sort / Radix sort / Bucket sort (0) | 2024.06.01 |
| [ 알고리즘 ] 21. Comparison sort (0) | 2024.05.31 |
| [ 알고리즘 ] 20. Quick sort (0) | 2024.05.27 |




