오래 못 할 짓 하지 않기
[ 알고리즘 ] 24. String match 본문
1 . Basic Algorithm
2. Rabin - Karp Algorithm
3. String matching with finite automata
Basic Algorithm

String Matching
주어진 Text T에 Pattern P가 들어가는지 판단하는 것

T 의 길이는 n
P 의 길이는 m ( 아마 n보단 작거나 같아야 할 것 같다. )
P가 T에 있다면 Valid Shift라고 한다. or Invalid


4번줄 do if 도 반복문으로 돌아야 한다.
- 그에 대한 반복은 최소 1번 (첫 글자만 같은 경우)
- 최대 m번 돈다 ( 다 같은 경우 )
만약 m이 constant하다면?
m = n/2라고 하면 O(n^2)이 나온다.
만약 aaab라는 패턴이 있을 때
T에서 aaac이렇게 있다면
첫 반복에서 4번째 인덱스 , 그 다음 3 인덱스 ... 로 연속적으로 불일치가 일어나는 걸 알 수 있다.
하지만 컴퓨터는 그걸 모르고 냅다 들이박는다.
= Unefficient하다.
Rabin-Karp Algorithm
String length m → m digits Radix Num으로 바꾼다.
예를 들어 String 31425면 5번을 하나의 인덱스마다 비교해야하는데
Digit 31,425를 비교한다면 한 번만 하면 된다.
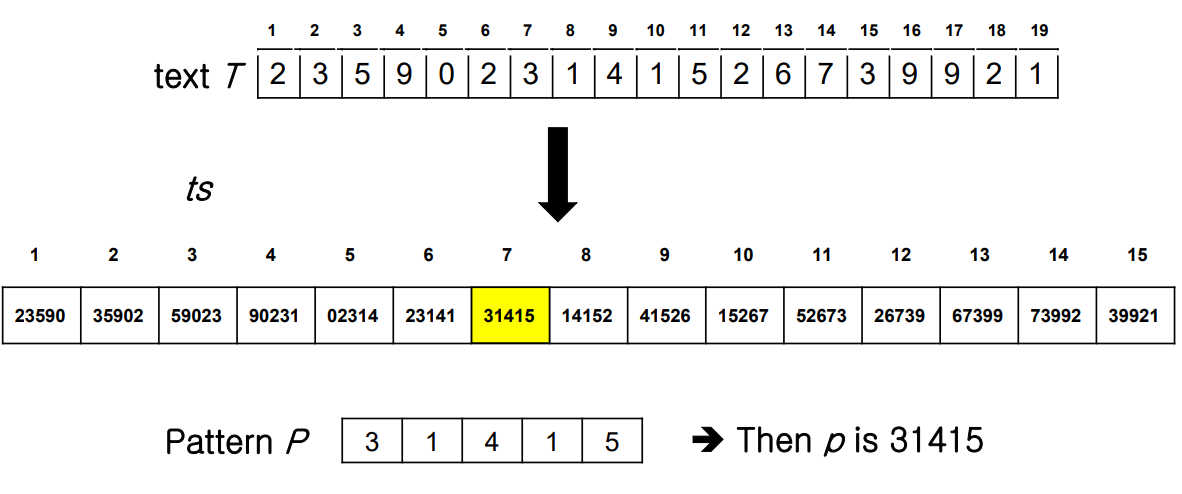
바꾸는 법은 Horner's rule을 적용한다.

그 다음에 오는 거 빨리 계산하는 법 ▼

제일 큰 자릿수 빼고
그 다음 인덱스 애를 더한다.
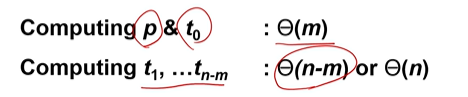
근데 이렇게 하면 좀 오래 걸리는 감이 있어서
모든 애들을 비교하는 게 아니라 mod(%)를 통해서
나머지가 같은 애들끼리만 비교한다.
물론 나머지가 같다고 무조건 비교하는 숫자와 같진 않지만
나머지가 다르면 무조건 다르기 떄문에
숫자가 같은 애들끼리만 비교한다.


적용 ▼
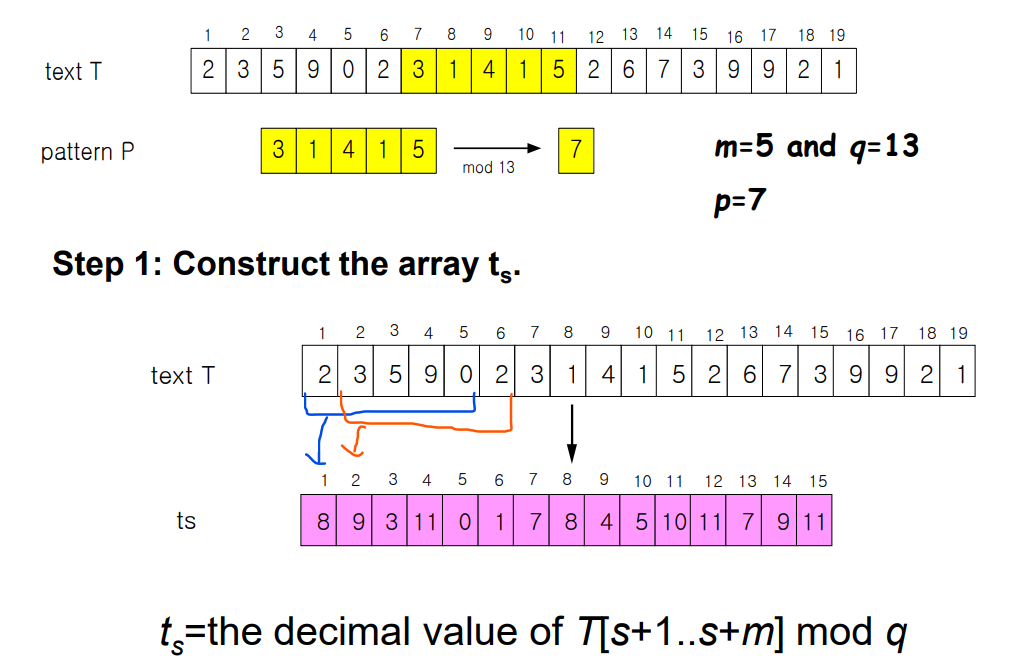
여기에서 7에 해당하는 애들만 비교한다.
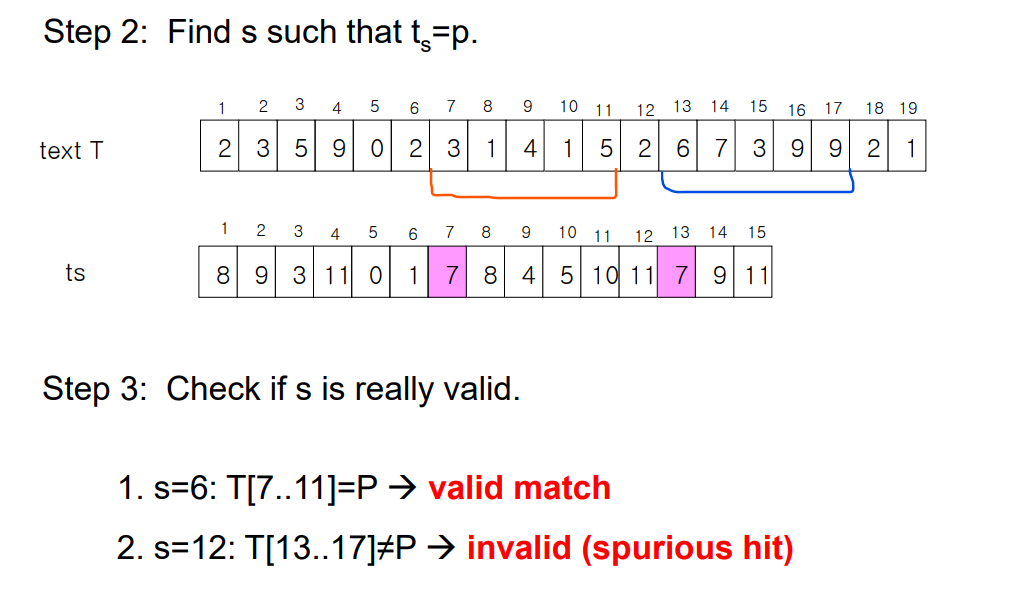
이렇게 할 때, 다음 숫자 빨리 계산해내는 법
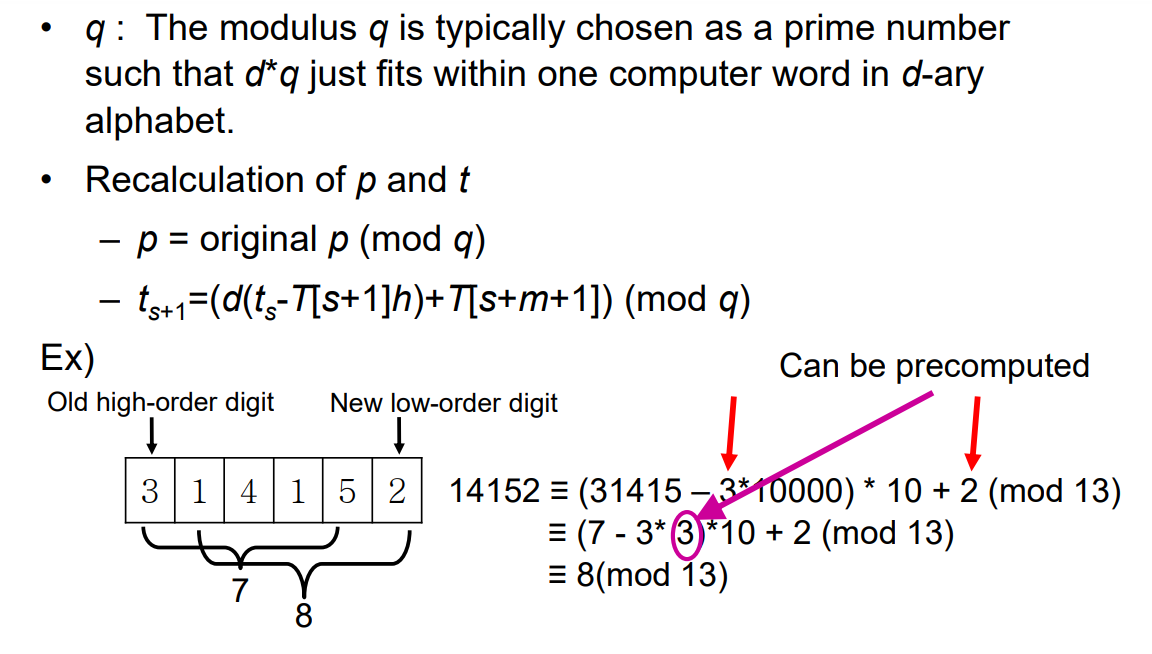
새로 나가는 숫자를 mod q해서 빼고
새로 들어오는 숫자를 mod q해서 더한다.
( 원래 숫자의 mod값 - 나갈 숫자의 mod값 ) * 10 (◀ 한 자리수 올려줘야해서)
+ 새로 들어오는 숫자의 mod
▲ 계산 해보기!!!

Worst case : 모든 애들의 mod값이 P와 같을 때 = Θ (n-m+1)
* valid인지 확인하는거 = Θ (m)
3. String matching with finite automata
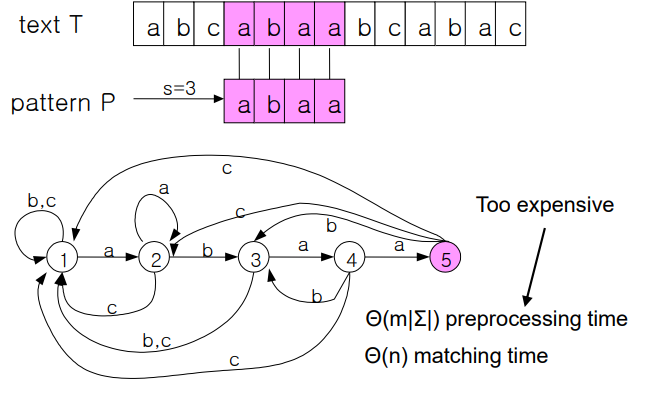
1에서 시작하고, 원하는 게 나오면 5에 도착하는 구조를 만든다.
논리 설계 State diagram이라고 생각하면 된다.
근데 이거 만드는데 좀 오래 걸려서 좋진 않음.
이 정도만 알고 넘어가자
(출처)
한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 25. String matching 2 - KMP (0) | 2024.06.11 |
|---|---|
| [ 알고리즘 ] 23. Medians and Order statistics (0) | 2024.06.04 |
| [ 알고리즘 ] 22. Counting sort / Radix sort / Bucket sort (0) | 2024.06.01 |
| [ 알고리즘 ] 21. Comparison sort (0) | 2024.05.31 |
| [ 알고리즘 ] 20. Quick sort (0) | 2024.05.27 |




