오래 못 할 짓 하지 않기
논리 설계 12 (Carry look ahead adder) 본문
Carry look ahead adder
- 사용하는 이유 : 시간 절약
Propagation delay + carry out 주는 것까지 계산하는 시간을 생각하면 너무 길다.
그러므로 해당 게이트에서 정확한 값보다는 자리올림이 발생하는지만 파악 할 수 있는 식을 만든다.
따라서, AB = (Cin이 없을 때 carry out이 있는지 ) 혹은 (+) A xor B ( Cin이 있을 때 carry out이 있는지)를 확인하여 시간을 절약
+
AB = Carry generator = 캐리 받은 거 없는데 만들어 내서 G(generator)라고 부름
A xor b = Carry propagation = 캐리 '받고' 만들어내는 놈이라서 P(propagation)라고 부름
Critical Path = [ 전체 회로에서 가장 오랜 딜레이를 유발하는 path]
즉 최장 딜레이 경로

하나하나 설명해주면
p: carry propagation
AB=10 또는 01일 때, Cin=1이면 Cout=1이다 (둘이 다를 때 = 둘 중에 하나가 1)
carry가 전달되었다는 의미로, p = A+B이다
OR 대신 XOR로 치환해 써도 된다
g: carry generator
AB=11일 때, Cin이 무엇이든 Cout=1이다
carry가 생성되었다는 의미로, g = AB이다.
c(i+1) ( = Cout) : G(i)+P(i) * C(i)
G나 P*Cin중에 하나만 1이어도 자리 올림이 발생했다는 뜻이므로 이런 식이 나옴
S(i) = P(i) XOR C(i) = Ai Xor Bi Xor C(i-1) 임
A,B 두 개가 다르면 1이고, 그걸 T라고 해보자
T =0(둘 다 같은 수) , C = 0 → S = 0
T =0(둘 다 같은 수) , C = 1 → S = 1
T =1(둘 다 다른 수) , C = 0 → S = 1
T =1(둘 다 다른 수) , C = 1 → S = 0
C 구해보기

C1 즉 C0에서 생긴 Cout은 이렇게 만들어진다.
이 C1이 다음 회로의 Input 중 하나가 될 것이다.
그 식은

이 식일 것이고, C1에 C1의 우변을 대입하면


이런 식이 나온다.
큰 표로 보면
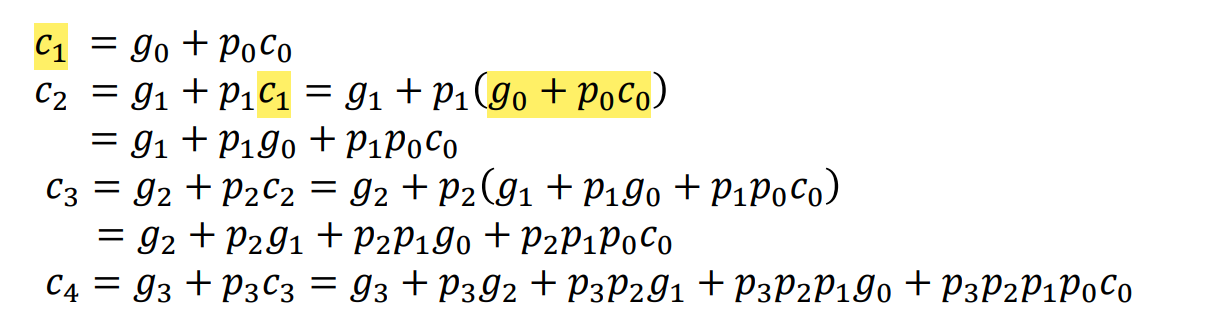
이렇게 표현됨.
이 식을 회로로 그렸을 때
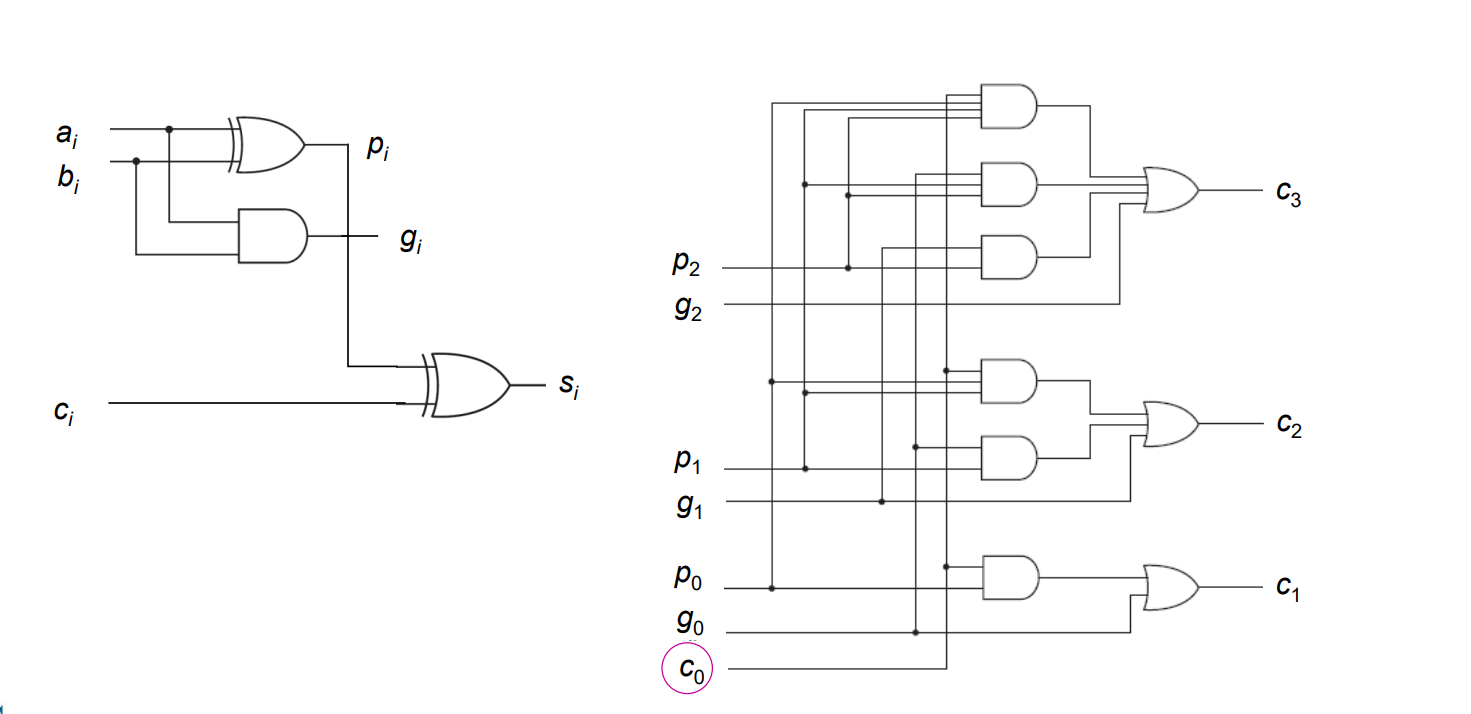
이런 회로가 나오는데 가장 밑 회로에서는 C0*P0 + g0 임 올라갈 수록 복잡해지긴하는데 일단 보는 법만 알아두기
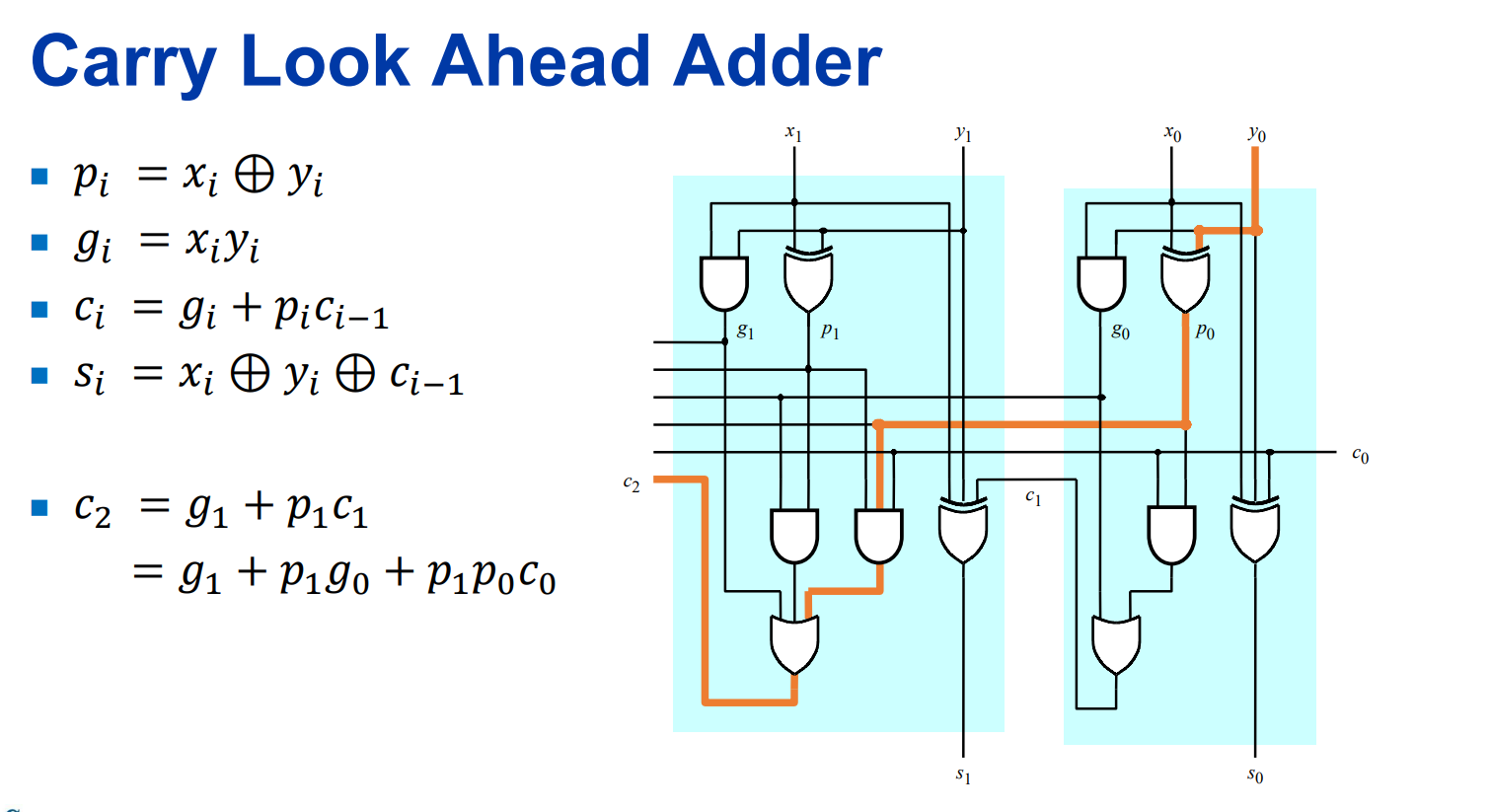
이것도 아직은 이해만 해놓자
[출처] Carry LookAhead (CLA) Adder로 딜레이 개선|작성자 뉴터
https://blog.naver.com/haran3056/222898833162 <<잘 알려주
한동대학교 고윤민교수님 - 논리설계 PPT
'2학년 1학기 > 논리 설계 ( Logic design )' 카테고리의 다른 글
| 논리 설계 14 (0) | 2023.04.14 |
|---|---|
| 논리 설계 13 (Comparators , Encoder / Decoder ) (0) | 2023.04.11 |
| 논리 설계 11 (Combinational Logic Circuits = 조합 논리 회로) (0) | 2023.04.05 |
| 논리 설계 10 (콰인 - 맥클러스키 방법 - table , Don't care) ( 사진 안 뜸 ) (0) | 2023.04.04 |
| 논리 설계 9 ( 카르노 맵 - POS , 변수 5,6개 , 출력 2개인 회로 간단화 , 콰인-맥클러스키 방법 ) ( 사진 안 뜸 ) (0) | 2023.04.01 |




