오래 못 할 짓 하지 않기
[ 알고리즘 ] 15. DFS 활용 - Bi - Connected Component 본문
BI - Connected Component
: Undirected + Maximal biconnected subgraph
● Articulation Point
: Vertex V가 사라졌을 때 하나의 Component가 2개로 나눠질 때!
해부학적으로는 '관절'이라 생각하면 될 것 같다.
= 다리에서 무릎 관절 역할!

▶ BI-Connected 라는 것은
하나의 Vertex가 사라져도 하나의 Component가 분해되지 않는 것!!


위 그래프는 Bi-Connected가 아니다.
이걸 쪼개면 오른쪽같은 단위로 쪼갤 수 있고, 그만큼이 Articulation Point라는 뜻이므로
Articulation Point가 존재한다는 건 Bi-Connected가 아니라는 것!


이렇게 생긴 Tree에서, z의 Subtree 중에서 Back edge가 없다면
y는 articulation Point이다.
찾는 방법
▶ Discovery Time으로 찾는다.

1. 하나의 Vertex를 DFS 방법으로 Discovery Time을 체크한다.
2. 본인의 Back edge를 만났을 때,
Back 이라는 변수에 현재 설정된 본인의 discovery time과
그 edge로 갔을 때 있는 vertex의 discovery time중에 작은 것을 고른다.
3. Back tracking할 때,
U의 Back과 V의 Back을 비교해서 작은 것을 고른다.
back v가 더 작다는 것 = vertex u 없어도 그 위에 애들로 갈 수 있다.
그래서 흐름은 다음과 같다.
내려갈대로 내려간다.
i) 만약에 본인이 마지막 vertex이고, back edge가 없다?
▶ 3번 back tracking 만 적용됨.
ii) 있다?
▶ 2,3번 조건에 들어가서 다 비교하고 나옴.
u의 back 값은 w의 discovery time이 된다.
의미는 u 본인의 subtree 중에서 3인 vertex까지 갈 수 있다.
그러므로 그 사이에서는 끊겨도 Bi-connected이다.
[ Back 변수의 역할 ]
: 여기로 계속 파고가면 나중에 #의 dicovery time을 가진 vertex로 갈 수 있다.

예제 1)

u부터 DFS로 간다고 했을 때
discovery time은 다음과 같다.
첫 번째로 각 노드의 back 값은 자신의 discovery time으로 초기화된다.
그렇게 y까지 갔을 때, y는 v와 연결되어 있으므로
back의 값은 min(본인의 discovery , 연결된 vertex의 discovery) 으로 설정한다.
= min(5,2) = 2

그리고 y에서 backtrack을 하면서 각 vertex들과 back 값을 비교하여 작은 값으로 업데이트 해준다.
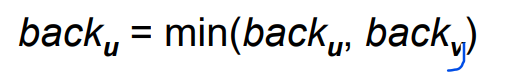
* u는 위에 있는 vertex들을 뜻한다.
결과 ▼

v vertex가 없으면 component가 2개로 나눠진다.
= Bi-connect X

하지만 Tree의 Root는 Articulation이라고 할 수 없다.
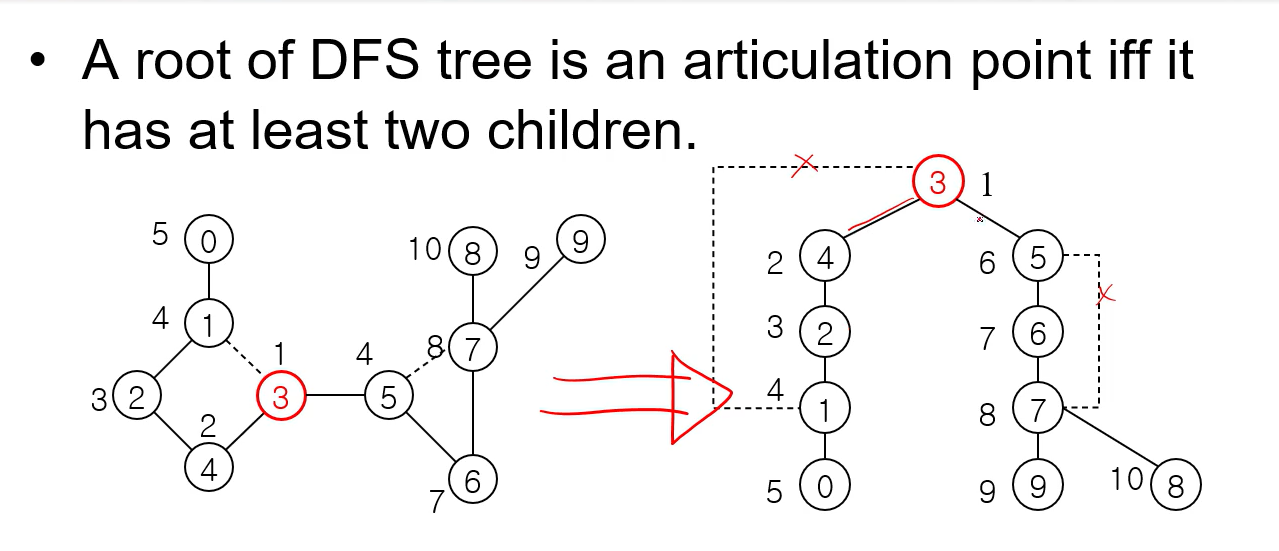
이렇게 2개의 Children을 가진다면 Articulation이라고 할 수 있다.
예제 2

답▼

C에 대해서는 B가 Articulation pt가 아닌데, D에 대해서는 맞음
(출처) 한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 17. Shortest path (0) | 2024.05.14 |
|---|---|
| [ 알고리즘 ] 16. Minimum Spanning Tree (0) | 2024.05.12 |
| [ 알고리즘 ] 14. DFS 활용 - Critical Path ( 최장 경로 ) (0) | 2024.05.06 |
| [ 알고리즘 ] 13. DFS - 활용 (0) | 2024.04.29 |
| [ 알고리즘 ] 12. DFS (0) | 2024.04.28 |




