오래 못 할 짓 하지 않기
[ 알고리즘 ] 16. Minimum Spanning Tree 본문
참고
https://min-h-study-review.tistory.com/54
Minimum Spanning Tree
조건
: Connected + Undirected + Non-Cycled + Weighted graph
이 중에서도 우리는 모든 Vertex를 지나고 , Total Weight가 최소인 Tree를 구할 것이다.
● 특징 )
1. n개의 vertex / n-1개의 Edge
2. MST 가 Unique하지 않을 수도 있음.

(a)에 대한 MST는 b,c 두 개가 있다.
● MST를 찾는 알고리즘
:
1. Kruskal Algorithm
( 가장 Weight이 낮은 Edge부터 하나하나 가져옴 )
2. Prim Algorithm
( root Vertex 에서부터 인접한 Edge중에서 Weight 가 낮은 걸 선택 )
모두 Greedy 알고리즘이다.
일반적인 방법의 MST를 구하는 방법.
1. A 라는 Edge set을 만들고, empty로 초기화 시킨다.
2. A에 Edge를 더하는데, A는 MST의 subset이라는 Loop invariant를 유지해야한다.
*loop invariant : 반복문을 계속 돌아도 변하지 않는 성질
▶ A가 MST의 Subset이다 = (u,v) edge는 Safe edge이다.
* Safe edge : A에 해당 edge를 더하더라도 MST를 유지하는 edge
수도코드는 다음과 같다.
A라는 박스에 Edge를 담는데,
지금 담으려고 하는 Edge가 'A Tree에 대해 safe edge면 추가'.
● Safe edge 찾는 법
Tree V를 disjoint 하게 나누는 cut을 찾아라.
하나의 집합을 S라고 했을 때, 그 외 집합을 V-S라고 할 수 있고,
그걸 나누는 선을 Cut이라고 한다.

초록색 = S
흰색 = V-S
빨간선 = Cut
Cut을 지나는 Edge들을 Cross 한다고 말함
Light Edge
: Cross Edge 중에서 Weight가 Minimum인 것
주로 Cycle이 되었을 때, Cross Edge중에서 Light Edge를 남긴다.
* unique하지 않을 수 있음

파란색 Edge를 A에 담는다고 해보자.
이 3개의 Edge중에서 Cut를 Cross하는 Edge는 존재하지 않는다.
이럴 때 A는 Cut 을 Respect한다고 한다.
Theorem


T 가 A를 포함하는 MST라고 하자.
( u , v ) 는 Light Edge라고 가정했을 때,
1. T는 Edge A를 포함했지만, ( u,v )는 포함시키지 않았다.
2. 그럼 우린 T' = T + (u,v) 를 만든다.
3. 근데 그렇게 했을 때 T' 는 Cycle 형태가 되므로,
Cut을 만들고, Cross edge중에서 Light Edge가 아닌 것을 지운다.
T' = T' - ( x,y )
Weight (x,y) >= Weight (u,v)

Kruskal algorithm
개념
- Edge 를 Weight 가 낮은 순서대로 정렬한다.
- 매 반복마다 가장 낮은 Weight를 가진 Edge를 선택한다.
> 골랐을 때 Cycle 이 되지 않는다면 선택 / 그렇지 않다면 Discard한다.
+ 매 반복마다 (Connect Component 끼리 or Tree와 Tree) Cut을 정의하고,
그 사이에 있는 Light Edge 선택하여 Merge한다.
Cycle이 되지 않는다는 걸 판단하는 방법
: 해당 Edge로 이어진 Vertex가
같은 Connected Component에 있는지 알아낸다.


Graph = E
F (바구니) = 0
Graph에서 계속 빼낼건데, 그게 안이 다 비어있지 않았다면 반복
▶ R에서 light edge를 꺼낸다.
▶ 지금 꺼낸 Edge가 F에 들어갔을 때 Cycle을 만들지 않는다면 ??
F에 해당 Edge 추가.
F를 Return
예제1

이런 Graph가 있다고 해보자.
현재 상황 :
● F = 0
● Light Edge = ( B, E )
> F에 넣었을 때 Cycle?
→ X , 그럼 F에 추가
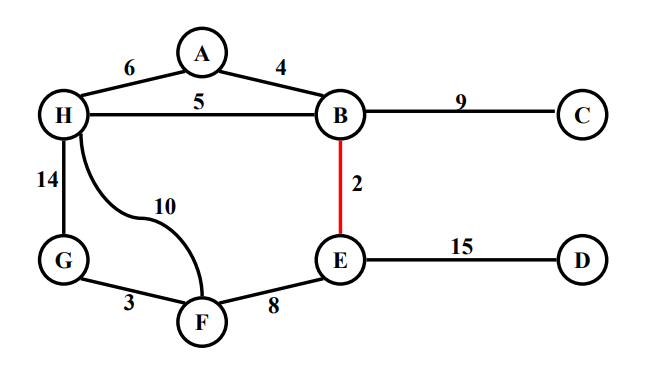
현재 상황 :
● F = (B,E)
● Light Edge = ( F , G )
> F에 넣었을 때 Cycle?
→ X , 그럼 F에 추가

...

현재 상황 :
● F = (B,E) , (F,G) , (A,B) , (B,H)
● Light Edge = ( A,H )
> F에 넣었을 때 Cycle?
→ O , 그럼 Discard.
...
결과 :

Prim algorithm
: 전체 Tree V에서 Root Vertex 선택
▶ 현재 Vertex(Tree)에 이어져 있는 Cycle이 되지 않는 Light Edge를 선택
= [ 현재 만들어진 Tree = Va ] , [ V- Va ] 사이에 있는 Light Edge를 선택
▶ 반복...
+ vertex r의 Parent 는 ㅠ[r] 로 나타낸다.
● 특징
- Light Edge를 빨리 찾기 위해 Priority Queue를 사용한다.


- 모든 Vertex를 Unseen 상태로 둔다.
- root vertex를 정해서 거기서부터 시작한다. = 얘를 Tree에 넣음
- 그 Tree랑 연결된 Vertex는 Fringe로 넣는다.
반복 : Fringe vertex가 있다면
▶ Fringe vertex와 현재 Tree 사이에 Minimum weight edge를 선택한다.
▶ v에 Minimum weight edge를 추가한다.
▶ 새롭게 정해진 Tree v에 adjacent vertex 들을 Fringe로 바꾼다.
예제1

다음 그래프에 대한 문제를 보자
A를 Root로 시작한다.

A를 Tree에 넣고, A와 연결된 Vertex 들을 Fringe에 넣는다.
▶ Fringe 에 있는 Vertex와 A사이에 Cut을 만든 후, Light Edge를 선택한다.
▶ 그 Edge와 연결된 Vertex를 Tree에 넣는다.
(그게 (c) 임 )
...

여기에서 A - F , 정확히는 Tree와 F는 Weight가 7이었는데
이 다음 단계를 보면 F와의 거리가 5가 된다.

우리는 항상 Vertex와 Tree 사이의 Weight를 고려해야한다!
결과 ▼


- 모든 Vertex를 Priority Queue에 넣는다.
- 반복문 : Queue안에 있는 Vertex의 [ Key값은 무한대 ] 로,
[ 자신의 부모는 없다 ] 고 초기화한다.
- root 의 key값은 0 , parent X
- 반복문 : Q가 비어있지 않았다면
▶Queue에서 하나 꺼내서 u에 담는다.
▶ 반복문 : u와 인접한 것들을 v로 하여 이에 대해 반복한다.
▶ 만약 현재 나와있는 Weight(u,v) 이 Key[v] 값보다 더 작으면
▶ v의 부모는 u , key[v]는 w(u,v)로 바꾼다.

여기에서 u와 인접한 vertex에 대한 Weight은 3,14이다.
그럼 마지막에 있는 조건문은 [ 3 < 무한대 ] + [ 14 < 무한대 ]
이렇게 했을 때 ㅠ[3] = ㅠ[14] = u이고,
key는 각각 본인들로 가는 weight이다.
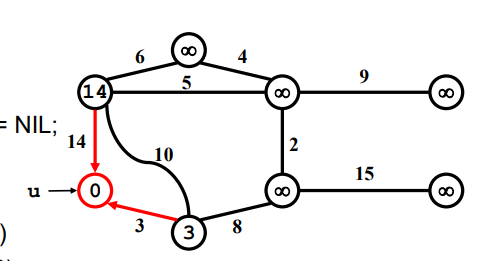
또 한 단계 더 가면
다음과 같다.

8은 볼 거 없음.
10 기준에서 봤을 때, 원래 14였는데
조건문 들어가보면 10 < 14 이므로 바꿨음
부모도 3인 노드로 바꿈
원래 그림엔 Direction이 없음. 부모 나타내려고 한 거임
여기 나온 예제들 다 해보자
(출처) 한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 18. Shortest path - Dijkstra Algorithm (0) | 2024.05.18 |
|---|---|
| [ 알고리즘 ] 17. Shortest path (0) | 2024.05.14 |
| [ 알고리즘 ] 15. DFS 활용 - Bi - Connected Component (0) | 2024.05.10 |
| [ 알고리즘 ] 14. DFS 활용 - Critical Path ( 최장 경로 ) (0) | 2024.05.06 |
| [ 알고리즘 ] 13. DFS - 활용 (0) | 2024.04.29 |




