오래 못 할 짓 하지 않기
[ 알고리즘 ] 17. Shortest path 본문

u에서 v까지 가는 Shortest path의 Weight은
[ Path가 존재한다면 ]
u → v까지의 path의 weight의 최솟값을 구한다.
[ Path가 존재하지 않는다면 ]
무한대
길 찾기의 유형
1. Single source shortest path
: 하나의 Vertex에서 다른 모든 Vertex로 가는데 가능한 최단 경로
(이거 먼저 배울거임)
● 알고리즘
- Bellman-Ford Algorithm
- In DAG
- Dijkstra's Algorithm
2. All- Pair shortest path
: 모든 Vertex에서 모든 vertex까지 가는데 가능한 최단 경로
● 알고리즘
- Floyd - Warshall Algorithm
(다음 장에서 배움)
Shortest path
● 특징
- Optimal substructure 가 성립함
- Negative Weight edge는 Cycle이 없다면 가능함
- Shortest path에서는 Cycle이 존재할 수 없다.

Shortest path algorithm
Source vertex s에서부터
모든 Vertex인 v까지 가는데 필요한 정보

d[v] = S에서 V까지 지난 거리
ㅠ[v] = s에서부터 오는데 거쳐온 v의 predecessor ( = 내 전에 누구임 )
Relaxation
: d[v]의 Upper bound 를 유지시키는 것이다.
원리는 간단하다. 처음에는 무한대로 설정
그거보다 작은 값이 나오면 그걸로 변경
▶ 반복...
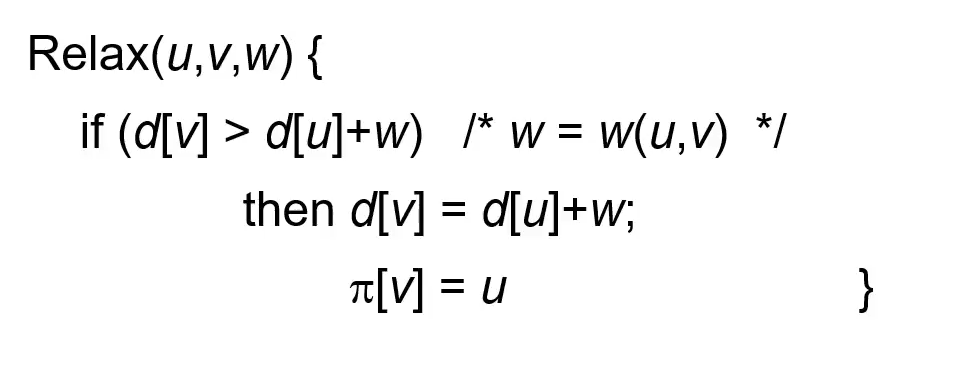
v까지 가는 길은 d[v]가 가장 작다고 알려져 있었다.
근데 d[v] 값보다 u까지 가서 edge하나 타고 가는 것 ( =d[u] + w ) 이 더 작다고 발견되면
d[v]를 그 값으로 바꾸고 부모는 u로 바꾼다.

Bellman - Ford algorithm
● 가장 제약조건이 적다.
- Weight이 negative여도 가능 / Cycle은 안 됨

1. Source 초기화
: 모든 d[ @ ] = 무한대
모든 ㅠ[ @ ] = NIL
d[ s ] = 0
2~4 : Edge Weight 계산
: ( Vertex 개수 -1 ) 만큼 돌면서
각 Edge사이를 왔다갔다 하면서 Relax를 한다.
Time complexity = 세타 (| V | -1 ) * E = 세타 (VE)
5~7 : Negative weight 있으면 False return
: 위에서 Relax를 다 했는데도 계속 돌면서 Relax가 된다?
Negitive weight cycle이 있다는 뜻이므로 False를 Return
● 예제 1)
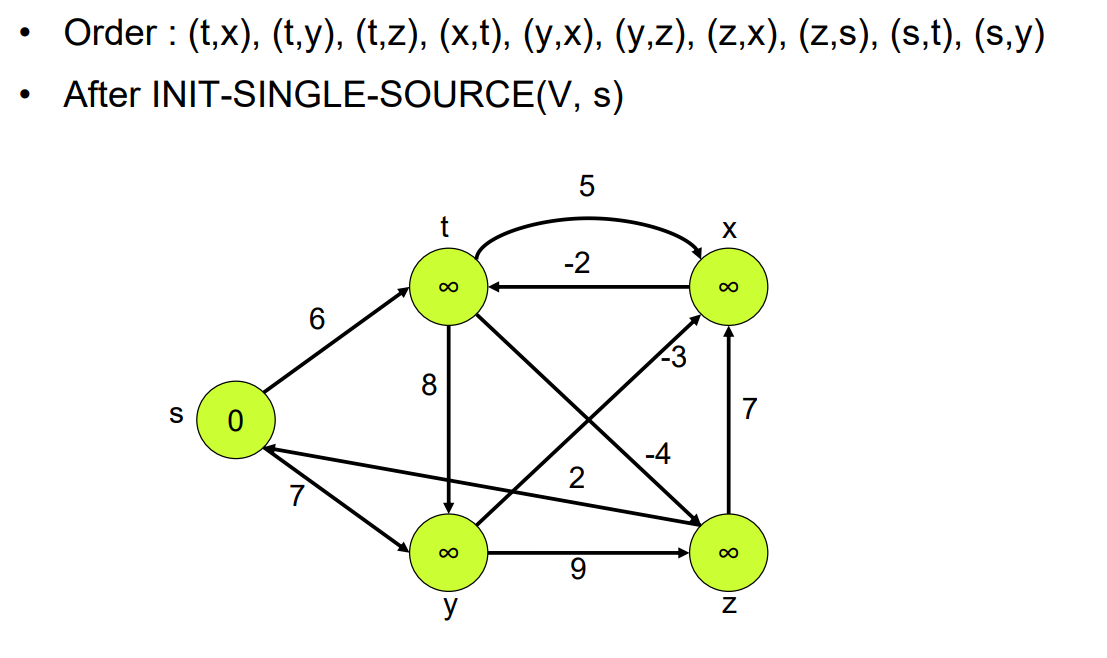
한 두 개 정도만 예시보여주겠음
- (t,x) 먼저
d[x] = 무한대
d[t] + 5 = 무한대+5
둘은 같으므로 변하지 않는다.
... 계속 똑같음
- (s,t)
d[t] = 무한대
d[s] +6 = 6
새로 발견된 게 더 작으니 d[t] = d[s] +6 으로 업데이트한다.
- (s,y)
d[y] = 무한대
d[s] +7 = 7
새로 발견된 게 더 작으니 d[y] = d[s] +7 으로 업데이트한다.
이렇게 한 사이클이 돌아갔고, 다시 처음으로 돌아간다.
- (t,x) 먼저
....
...
결과

한 번 해보자
● 예제 2)

Edge가 가장 위에 있는 게 -5로 바뀜
한 번 풀어보셈
DAG
● Topological sort를 사용한다.
- DAG에는 Cycle이 없기 때문에!
Topological Sort를 하면 왼쪽에서 오른쪽으로 정렬이 되기 때문에
그냥 한 번만 슥- 돌면 끝난다.
예제 1)
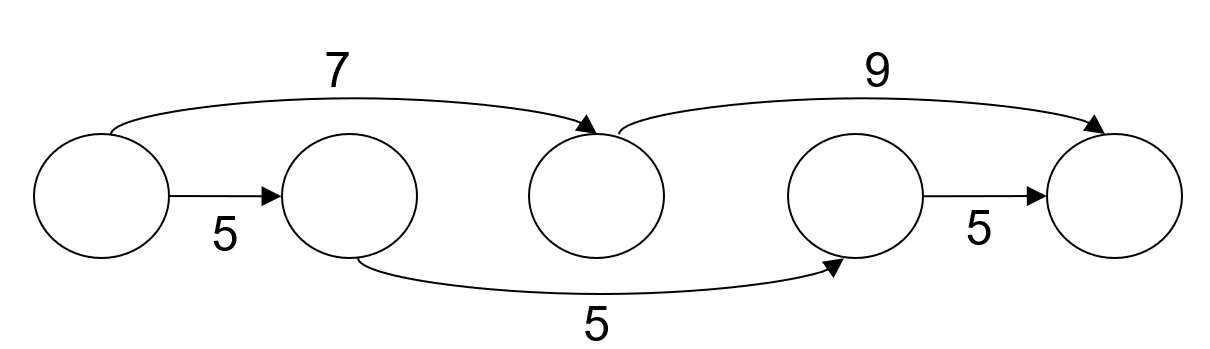
Init한다 ▼
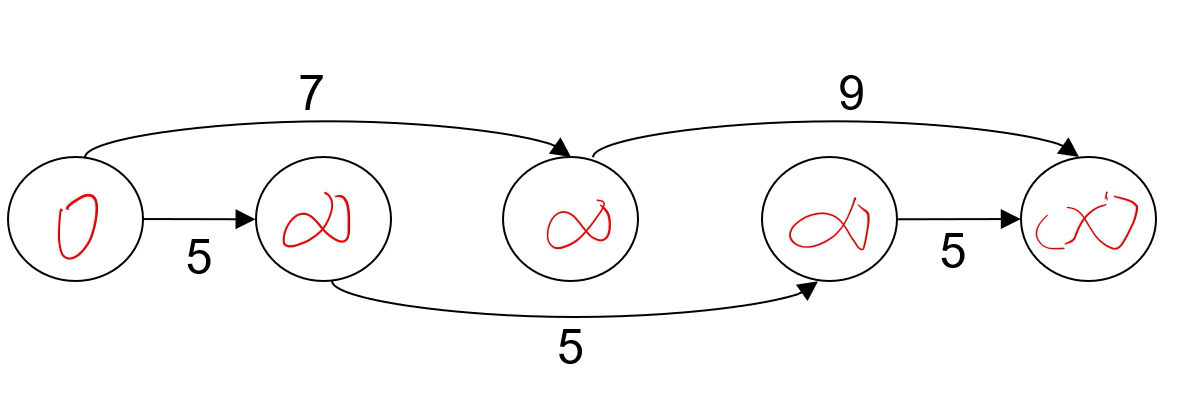
이제 왼쪽에서부터 오른쪽으로 Relaxation을 한다.
▼ Source vertex에서 한 번 돌았을 때 결과
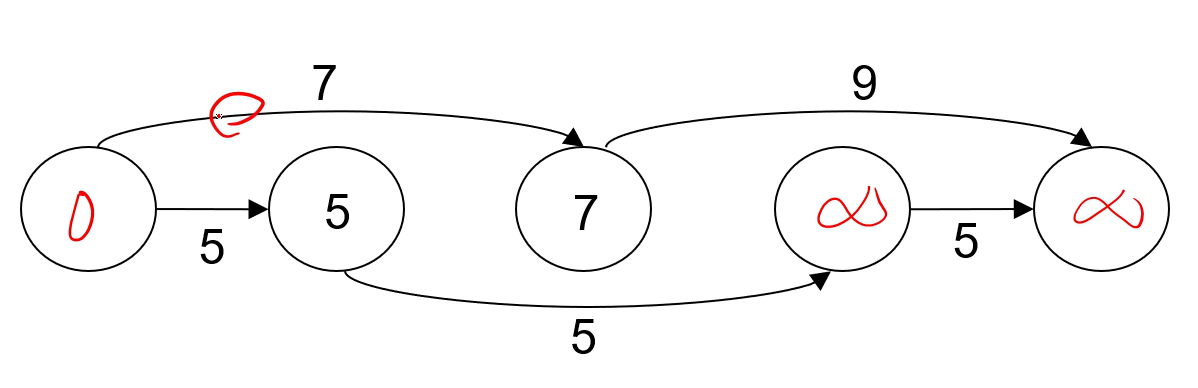
다 하면 이렇게 됨 ▼
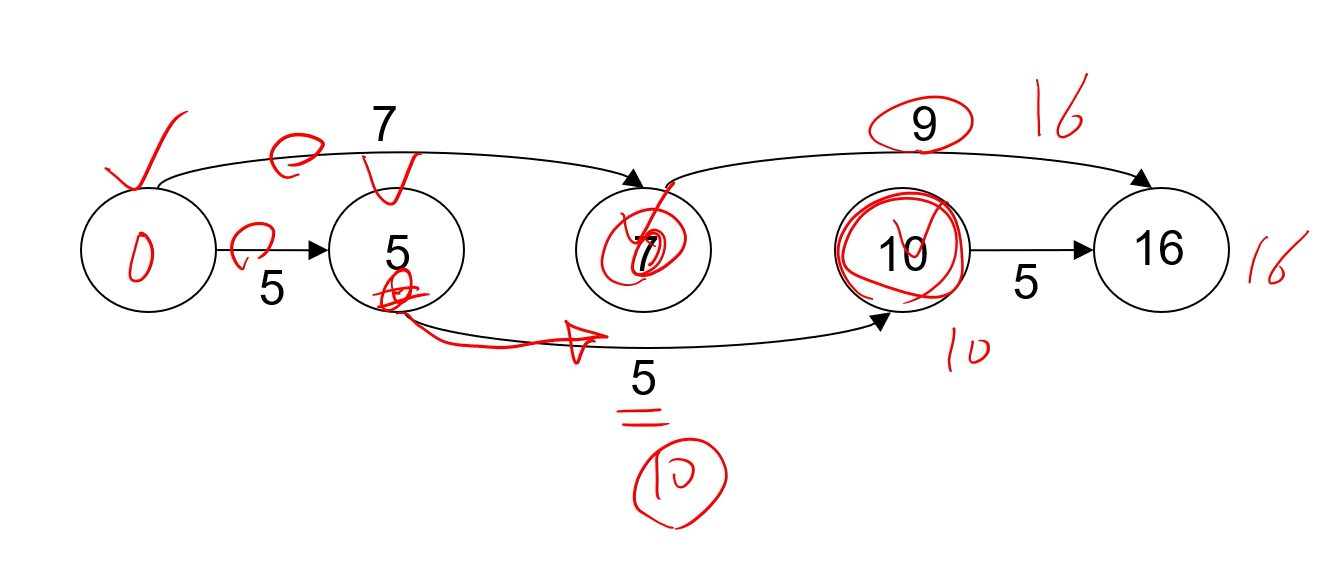

Topological 하게 Sort한 뒤에 Init까지 한다.
모든 Vertex u에 대해 sort된 order로
인접한 edge에 대해 Relax시킨다.
Time Complexity :
1. Topological sort : 세타 ( | V | + E )
2. Init : 세타 ( | V | )
3. Relaxation : 세타 ( | E | ) << vertex가 아니라 Edge에 대해서 실행하기 때문에
(출처)
한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 19. Floyd Algorithm (0) | 2024.05.21 |
|---|---|
| [ 알고리즘 ] 18. Shortest path - Dijkstra Algorithm (0) | 2024.05.18 |
| [ 알고리즘 ] 16. Minimum Spanning Tree (0) | 2024.05.12 |
| [ 알고리즘 ] 15. DFS 활용 - Bi - Connected Component (0) | 2024.05.10 |
| [ 알고리즘 ] 14. DFS 활용 - Critical Path ( 최장 경로 ) (0) | 2024.05.06 |




