오래 못 할 짓 하지 않기
논리 설계 26 (Simplification of Sequential Circuits) 본문
논리 설계 26 (Simplification of Sequential Circuits)
쫑알bot 2023. 6. 6. 13:10Simplification을 하기 위해 필요한 용어 3가지
- Equivalent - 같다.
- Seccessor - 후계자?( A에 입력으로 0을 넣었을 때 나오는 값 B --> A의 0 seccessor는 B이다)
- Partition - 그냥 나누는 거 ㅇㅇ
Equivalent

이 두 개의 상태는 같다고 표현함.
0101 했을 때 결과가 다 같음.

인풋 w = 0,1 일 때, 변화하는 Si(0일 때) , Si(1일 때) 이 두 개는 0/1의 successor 라고 한다.

파티션은 1개 이상의 블락으로 이루어져있음. 같은 것들끼리 묶는다고 생각하면됨. 근데 이게 또 계속 나누고 사이클 돌다보면 같지 않아질 수 있음.
우리는 Partitioning 하면서 식을 간단히 할 것임.
순서
1) 첫 P1 은 모든 식을 넣는다.
2) P1 --> P2 로 갈 땐 Output으로 두 개의 Partition을 만든다.
3) P2 부터는 각자의 Successor 들을 비교하여 한 Partition 에 있는 애들이면 Equivalent 로 처리.
아니라면 그 자리에 있었던 애를 다른 Partition으로 나눈다 (안 나눠질 때까지 나눔)
예)

1) 첫 P1 은 모든 식을 넣는다.
P1 = (ABCDEFG)
2) P1 --> P2 로 갈 땐 Output (0 , 1) 으로 두 개의 Partition을 만든다.
1 = ABD / 0 =CEFG
P2 = (ABD)(CEFG)
3) P2 부터는 각자의 Successor 들을 비교하여 한 Partition 에 있는 애들이면 Equivalent 로 처리.
아니라면 그 자리에 있었던 애를 다른 Partition으로 나눈다 (안 나눠질 때까지 나눔)
P2 = (ABD)(CEFG)
- (ABD)의 0 Successor = (BDB) --> BDB 는 ABD 의 Partition에 다 포함됨 --> Equivalent
- (ABD)의 1 successor = (CFG) --> CFG 는 CEFG 의 Partition에 다 포함됨 --> Equivalent
- (CEFG)의 0successor = (FFEF) --> FFEF 는 CEFG 의 Partition에 다 포함됨 --> Equivalent
- (CEFG)의 1-successor = (ECDG) --> ECDG 중에 D는 CEFG Partition에 다 포함 안 됨
--> ECDG 에서 D는 3번째 자리, CEFG에서 3번째 자리는 F.
따라서, F를 따로 뗀다. (CEG)(F)
P3 = (ABD)(CEG)(F)
- (ABD)의 0 Successor = (BDB) --> BDB 는 ABD 의 Partition에 다 포함됨 --> Equivalent
- (ABD)의 1 successor = (CFG) --> CFG 는 CEG 의 Partition에 다 포함 안 됨 (F가 나눠졌으니까) --> Equivalent
--> F가 있는 게 2 번째니까, ABD 두 번째에 있는 B를 따로 뗀다
--> (AD)(B)
- (CEG)의 0 successor = (FFF) --> FFF 는 F 의 Partition에 다 포함됨 --> Equivalent
- (CEG)의 1 successor = (ECG) --> ECG 는 CEG 의 Partition에 다 포함됨 --> Equivalent
P4 (AD)(B)(CEG)(F)
여기서는 더 해도 다른 거 없음.
결과 (AD)(B)(CEG)(F)

위 식을 가지고 이렇게 간단하게 바꿀 수 있다.
그 다음에 한 변수가 나오면 그 변수가 포함된 Partition에 있는 모든 걸 적는다.
처음에 A가 나왔으니 A가 있는 Partition에는 AD가 있으니 AD다 적는다.
w=0 일 땐 B , B가 있는 Partition에는 B밖에 없으니 B만 적는다.
w=1 일 땐 C, C가 있는 Partition에는 CEG가 있으니 셋 다 적는다.
이렇게 만들면 됨

n은 5센트 d는 10센트
15센트가 들어와야 candy 하나 줌.
--> d를 하나 넣어서 S2상태로 가면 15가 안 되었기 때문에 캔디없음
거기에서 5센트 하나 넣으면 S4로 가면서 사탕하나 나옴. 그렇게 받고는 다시 0원이 되니까 S1으로 이동.
각 S들마다 얼마 있는지. 캔디가 나올건지가 저장되어 있음
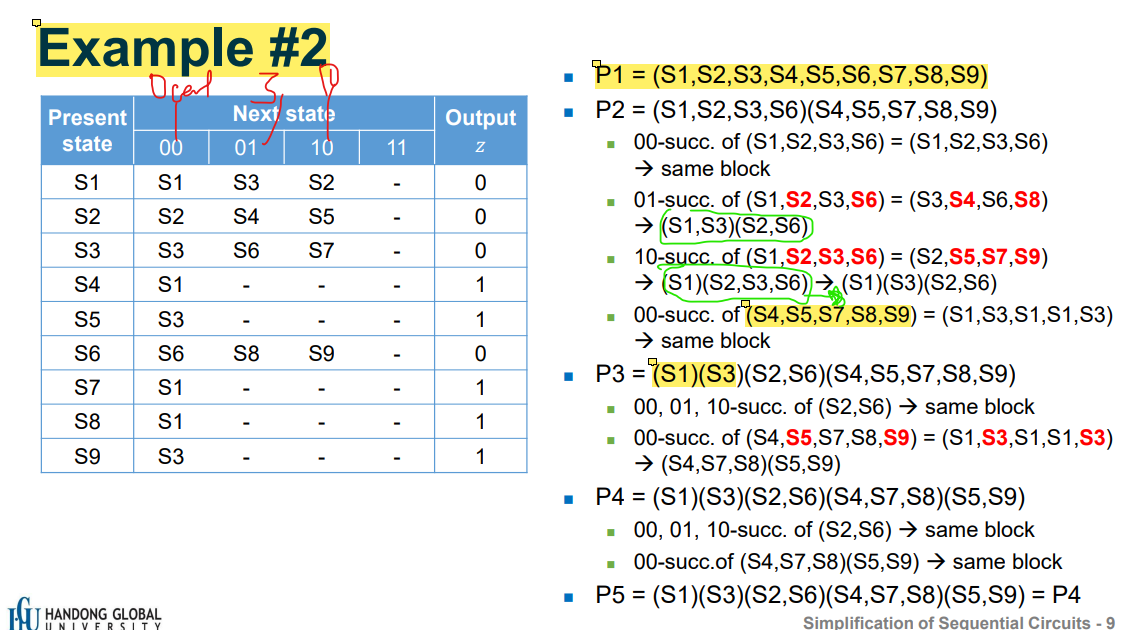
0원을 넣었으면 00
5센트를 넣어서 나오는 결과는 01
10센트를 넣어서 나오는 결과는 11
P3 에서 하나로 나눠진 애들은 succ 안 구해도 됨

이렇게 줄이면 됨

밀리머신 같은 경우에는 결과가 00 01 10 11 인지 나눠야함
아마 두 개로 주실 듯하다.
-인 경우에는 0으로 하든 1로하든 내 맘대로 정할 수 있다.
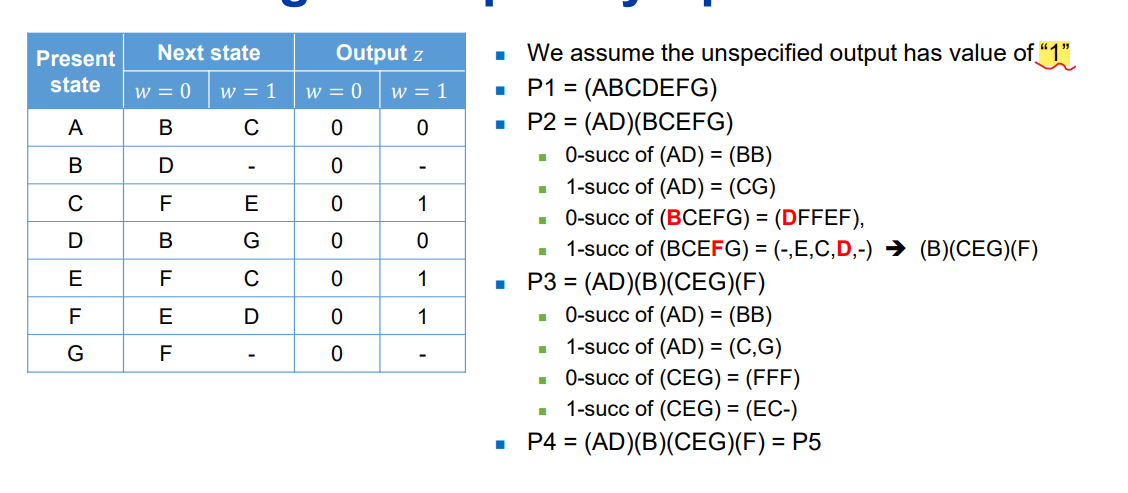
위와 같은 식인데 -를 1로 하느냐 0으로 하느냐에 다라 결과가 달라진다
출처: 한동대학교 고윤민교수님 -논리설계 PPT
'2학년 1학기 > 논리 설계 ( Logic design )' 카테고리의 다른 글
| 논리 설계 25 ( Chapter 8 ) (0) | 2023.06.04 |
|---|---|
| 논리 설계 24 ( Register , Counter ) (0) | 2023.05.30 |
| 논리 설계 23 (Asynchronous Counter , Register) (0) | 2023.05.27 |
| 논리 설계 22 (0) | 2023.05.26 |
| 논리 설계 21 (0) | 2023.05.21 |




