오래 못 할 짓 하지 않기
이산 수학 3 본문
Predicate
: 단정하다.
요소
1) 변수 : x, y, z
2) predicates = 단정할 문장(내 식대로 해석했음) : P(x) , M(y)
3) 수량/범위 : 모든 or 임의의
P(x1,x2,...,xn) : 'x1부터 n은 (P라는 문장)하다~ ' 라는 뜻임
P(q) : q>0이다.
...
P(-3)랑 P(0) 는 q가 0보다 작으므로 거짓
P(3)은 참
그냥 predicate는 판단문이라고 생각하면 된다.
그 안에 변수가 들어오면 , 그 변수가 P에 들어오면 참일까? 라고 판단하는 거

Quantifier
1. 모든 값에 대한 / For all / U / (A뒤집은 모양)
'>> 하나라도 True가 안 되는 게 있으면 False'
'== 반례가 하나라도 있으면 끝 '
2. 임의의 값에 대한 / There exists / E / (E좌우반전한 모양)
'>> 하나라도 True가 되는 게 있으면 True'
'== 되는 게 하나라도 있으면 끝 '

1. P(x) : x>0 이고, 범위는 모든 정수라면 =▶ Ux P(x) 는 false이다.
왜냐? 범위 내에서 반례가 하나라도 나옴. ex) -1
2. 는 범위가 모든 양의 정수라서 가능
3. P(x) : x는 짝수 , 범위는 모든 정수 → Ux P(x)는 false
왜냐? 범위 내에 반례가 있음 ex) 1,3,5,7

1. P(x) : x>0 이고, 범위는 모든 정수라면 =▶ Ex P(x) 는 True이다.
또한, U 가(전체 범위가) 양수라면 항상 True
2. P(x) : x<0 이고, 전체 범위는 양수라면 =▶ Ex P(x) 는 항상 False이다.
3. P(x) : x는 짝수 , 범위는 모든 정수 → Ux P(x)는 True
왜냐? 하나라도 만족하는 게 있으니까!

Loop를 돌면서 찾아보는 경우!
U : 반례가 하나라도 보이면 > Loop 중단
E : 가능한 게 하나라도 보이면 > Loop 중단

같은 P(x)에 대해서도 U이냐 E이냐에 따라 참 거짓이 달라진다.~

얘네 두 개가 웬만한 연산자보다 우선순위가 높음

Domain이 무한대가 아니라 정해져있다면 서로 이런 관계라고 할 수 있다
Domain (x= 1,2,3)
1) 모든 x에 대해 P(x)가 성립한다. = P(1) and P(2) and P(3) 가 참이다.
2) P(x)가 성립하는 x가 존재한다. = P(1) or P(2) or P(3) 가 참이다.
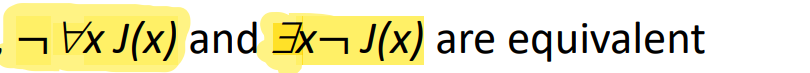
[ 모든 x에 관한 ] 의 inversion = [ x가 존재한다 ]
~ [ 모든 X에 대해 ] J(X)는 참이다.
= ~J(X)에 대해 참이 되는 X가 존재한다.
예)
' 모든 애들이 착한 것은 아니다'
= '어떤 애들은 착하다'


이렇게 두 개의 변수가 Quantification 이 있을 때 어떻게 계산이 되는지 확인하기
1) Ux Uy P(x,y) 일 때,
for ( int x=0 ; x< infinite ; x++){
for ( int y=0 ; y < infinte ; y++){
명제 판단
}
}
이렇게 하고, 어느 하나 P(x,y) 가 false → 바로 실행 종료
= Ux Uy P(x,y) 는 false다.
하나도 못 찾으면 그냥 끝까지 돌리고 끝냄
2) Ux E y P(x,y) 일 때,
x + +
y루프 돌리면서 , Ux E y P(x,y)가 참이 되는 짝만 찾으면 된다.
하나만 찾으면 바로 반복 끝
아니면 끝까지 계속 다 돌리고 끝낸다.
두 번째 자료 19 페이지부터 예시들 이해하고 계속보기
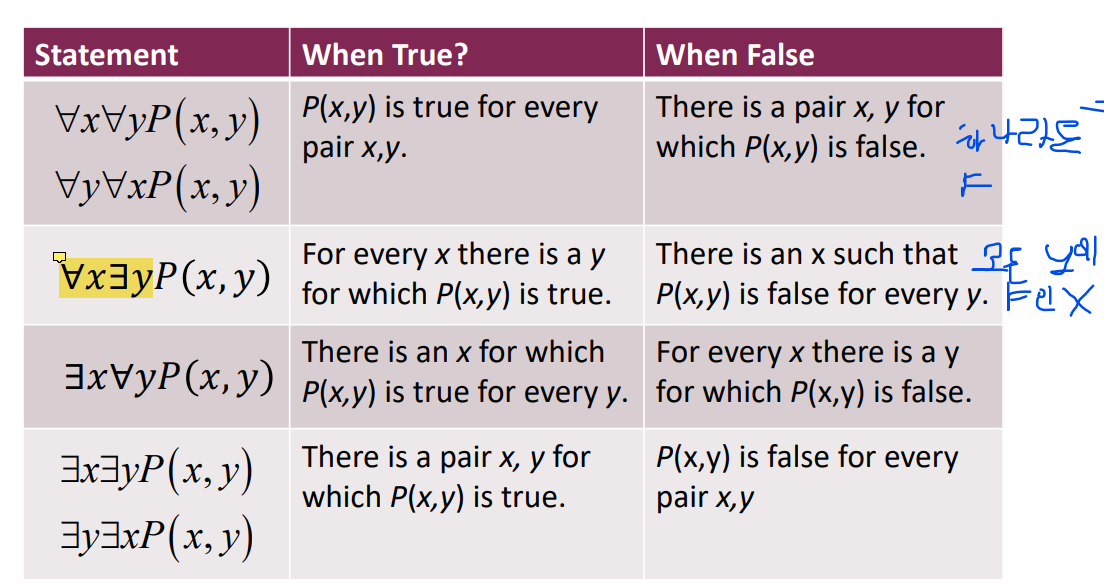
이 뒤에는 계속 다 예시랑 적용문제들임
시험 전에 이거 다 할 줄 알아야 함
출처 : 한동대학교 최희열교수님 - 이산수학
https://m.blog.naver.com/study_together_/221094765804
(출처2)
'2학년 2학기 > 이산수학' 카테고리의 다른 글
| [ 이산 수학 ] 6. 함수 (0) | 2023.09.16 |
|---|---|
| [ 이산 수학 ] 5. 집합 (고등학교 내용과 비슷함) (0) | 2023.09.12 |
| [ 이산 수학 ] 4. premises ( 전제 ) (0) | 2023.09.08 |
| 이산 수학 2 (0) | 2023.09.01 |
| 이산 수학 1 (0) | 2023.08.31 |




