오래 못 할 짓 하지 않기
[ 이산 수학 ] 11. 확률 본문
확률은 주로
- A가 일어날 확률 = [ A가 일어날 경우의 수 / 전체 경우의 수 ] 이런 형태이다.
경우의 수에 선택지가 2개 외에는 없을 때
E' = 1 - E 이렇게 해석된다.
(아래 예시에서 S는 전체 경우의 수)

예제1)

10비트 칸이 있을 때, 적어도 하나는 0일 확률은?
풀이)

E = 적어도 하나는 0인 경우
~E = 모두 1인 경우
따라서 " 1 - 모두 1일 확률 = 적어도 하나는 0인 경우 "
--> 모두 1일 확률 = 모두 1인 경우의 수 / 전체 경우의 수
경우의 수에 선택지가 2개보다 많을 때

그냥 집합의 덧셈과 같다.
각 확률에서 더하다 보니 중복해서 들어가는 부분이 있기 때문에
그 값을 한 번은 빼준다.

예제)

100 이하의 랜덤 숫자로 뽑았을 때 2나 5로 나눠지는 것일 확률은?
2나 5로 나눠지는 숫자일 확률 = 2로 나눠질 확률 + 5로 나눠질 확률 - 2나 5 모두로 나눠질 확률
= 50/100 + 20/100 - 10/100 = 3/5

S안에 있는 원소들을 s라고 했을 때,
1. 각 s가 일어날 확률은 0~1이라고 할 수 있고,
2. 그것들의 총합은 1이다.
예제 )

Heads 면과 Tail면이 있는 동전이 있고
Head가 나올 확률이 2배가 더 높다.
그럼 원래 동전인 경우 : p(h) = p(t) = 1/2인데
이렇게 하나의 확률이 높을 땐 p(h) = 2/3 , p(t) = 1/3이다.
(계산하는 법 : 하나에 변수,확률에 다 몰아준다.
p(h) = 2p(t)이다. --> p(h) +p(t) = 1 --> 2p(t) + p(t) = 3p(t) = 1
--> p(t) = 1/3 , p(h) = 2/3)
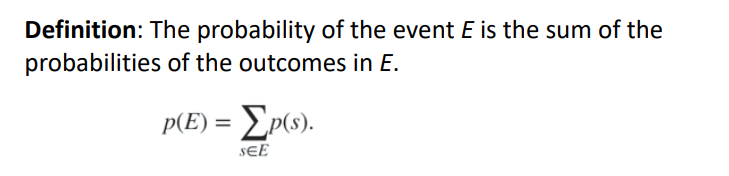
함수or집합 E에서 일어날 수 있는 확률
= 그 안에 있는 elements들이 일어날 확률의 합
예제)
3이 다른 것들에 비해 2배가 더 잘 나오는 주사위
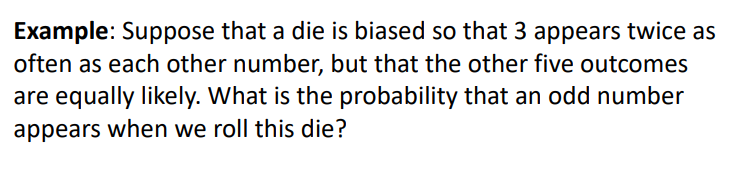
풀이
알아둘 것 1)
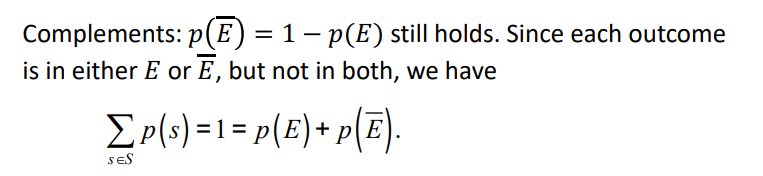
알아둘 것 2)
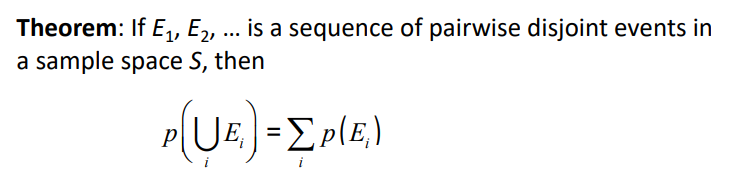
조건부 확률

P(구하고 싶은 거 | 조건 ) = 조건이 일어났을 때, 구하고 싶은 게 일어날 확률
P( E | F ) = F가 일어났을 때, E가 일어날 확률
예제 ) 0으로 시작하고, 적어도 2개 이상의 연속된 0이 있는 4비트가 나올 확

E = 연속된 0이 최소 2개 이상
F = 첫 비트가 0인 확률
Independent

E와 F가 independent인지 확인하는 법
[ p( E | F ) = p( E ) 인지 본다 ]
OR
[ p( E and F ) = p( E ) p( F ) 인지 본다 ]


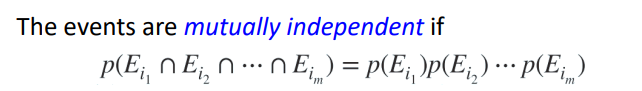

두 개의 결과만 가능한 상황에서 이거 or 저거 가 나올 수 있는데,
[이거 확률] + [저거 확률] =1임 (당연한 내용임)
예제)


b(k;n,p)
= n번 시행해서 . p의 확률인 event가 k번 나온 거
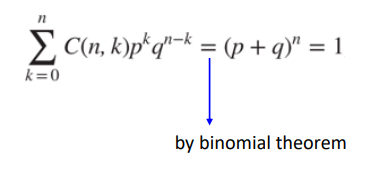
변수

X(s)에 있는 원소 r을 변수로 하여
그에 대한 식을 쓰는 거임
( r , r이 일어날 확률 )
예제)

X(t) = 동전을 3번 던졌을 때, 머리면이 t번 나왔다.
이런 식으로 변수를 쓴다. 주로 횟수나 개수를 변수로 설정한다.


방에 생일이 같은 사람이 있을 확률이 0.5 이하로 하게 하려면 최소 몇 명이 있어야 할까?
1년을 366일로 가정.
Pn = n명 중 2명이 다른 생일을 갖고 있다.
우리가 구하려고 하는 건 1- Pn임
- 2번째 사람이 첫번째 사람과 생일이 다를 확률 = 365 / 366
- 3번째 사람이 앞에 두 사람과 생일이 다를 확률 = 364 / 366
...
- n번째 사람이 앞에 있었던 사람과 생일이 다를 확률 = 366-(n-1)/ 366 = 367 - n / 366
P(n) = P(2)P(3)P(4)...P(n-1) 임
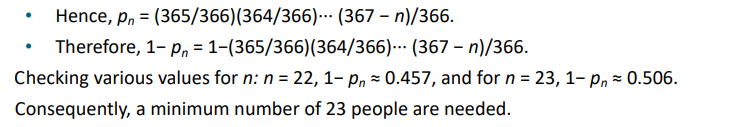
'2학년 2학기 > 이산수학' 카테고리의 다른 글
| [ 이산 수학 ] 13. 확률 분포 (0) | 2023.11.06 |
|---|---|
| [ 이산 수학 ] 12. 조건부 확률 2 (0) | 2023.10.30 |
| [ 이산 수학 ] 10. 경우의 수 (0) | 2023.10.13 |
| [ 이산 수학 ] 9. 재귀함수 / tree (0) | 2023.10.05 |
| [ 이산 수학 ] 8. 수학적 귀납 (0) | 2023.09.26 |





