오래 못 할 짓 하지 않기
[ 이산 수학 ] 12. 조건부 확률 2 본문
Bayes’ Theorem
p(E) ≠ 0 and p(F) ≠ 0 일때,

위 식이 성립한다.
이 식은 사실
= p( E and F ) / p( E and F ) + p( E and ~F ) // p( E and F ) + p( E and ~F ) = p( E )
이와 같다.
예제 )

박스 A = 초록공 2개 + 빨간공 7개
박스 B = 초록공 4개 + 빨간공 3개
이 때 하나를 뽑아서 빨간공이 나올 확률을 구하는 것이다.
E = 빨간공 선택
F = A박스 선택
우리는 p( F | E ) 를 구할 것이다.
우선 빨간공이 나오는 경우의 수는
1) 박스 A → 빨간공 (7/9)
2) 박스 B → 빨간공 (3/7)
이 있다.
따라서 p( 빨간 공인데 | 첫 번째 박스를 골랐을 때 ) = p( 박스 A 빨간공 ) / p( 박스 A 빨간공) + p(박스 B 빨간 공)
= ( 7/9 ) * ( 1/2 ) / ( ( 7/9 ) * ( 1/2 ) + ( 3/7 ) * ( 1/2 ) )
= 49 / 76

우선 정규 식은 위와 같고
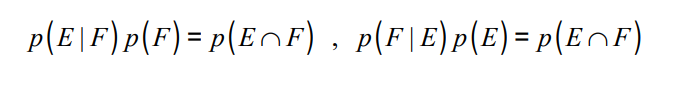
주로 활용할 때 ( p(F) or p(E)를 알고 있고, p( E and F)를 구할 때 )
이런 식을 많이 사용한다.
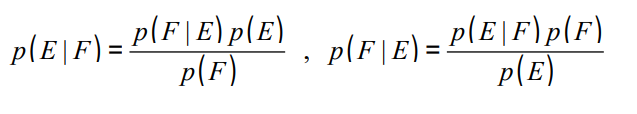
더 어렵게 활용하면 이러기도 함
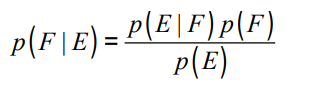
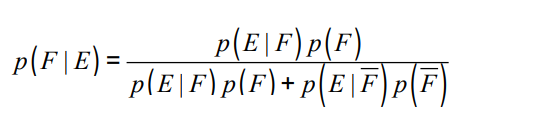
p( E | F ) * p( F ) = p ( E and F ) << 위 식에서는 변한 거 없음
p(E) = p ( E | F ) * p(F) + p( E |~F ) * p(~F)
= p ( E and F ) + p ( E and ~F )
따라서 위 사진에서 오른쪽과 같은 식이 나올 수 있음.
예제)

- 10만명 중에 한 명이 특정 질병을 가진다.
- 이 질병을 가지고 있으면 99% 양성이 나온다.
- 질병을 가지고 있지 않으면 99.5% 음성이 나온다.
a) 양성이 나왔는데, 질병이 있을 확률
b) 음성이 나왔고, 질병이 없을 확률
아래 주어진 힌트를 가지고 풀어보자.

p(D) = 질병을 갖고 있는 경우
p(E) = 양성이 나온 경우
우선 p( D and E ) 를 구해보자.
p(E|D) * p(D)
= 0.99 * 0.00001 = p( D and E )
p ( D | E ) = p( D and E ) / P (E) ( = (E and D) + (E and ~D) )
= p ( E | D ) * p( D ) / p ( E | D ) * p( D ) + p ( E | ~D ) * p( ~D )
= (0.99*0.00001) / (0.99 * 0.00001) + (0.005 * 0.99999)

b) 음성이 나왔는데 병이 없을 경우는?
[ 음성 + 병 O ] + [ 음성 + 병 X ] 인 경우에서
[ 음성 + 병 O ]인 경우
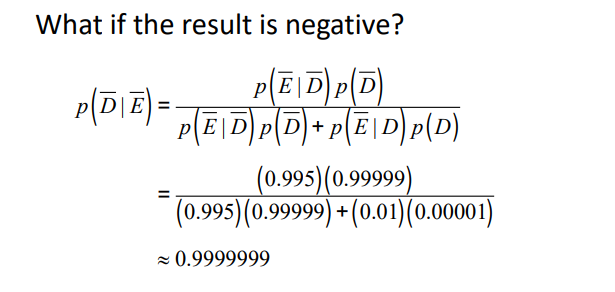

E는 그냥 이벤트 중에 하나, F는 각각의 고유한 (공집합이 없는) 이벤트이다.
(...교수님한테 컨펌받는 중...)
스팸 메일 필터 확률
지금까지 했던 걸 이용해서 생각해보면 아래와 같다.
S = 메시지가 스팸일 경우
E = 메시지에 w가 있을 경우
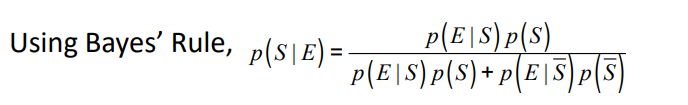
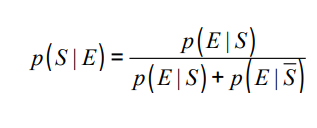
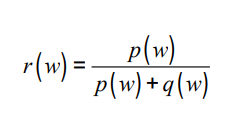
p(w) = w로 시작하는데 스팸
q(w) = w로 시작하는데 스팸 X

Rolex라는 단어가 250/2000 꼴로 스팸 메시지.
5 / 1000 꼴로 스팸X 메시지로 나타난다.
Rolex라는 단어가 포함되어 있는데 스팸일 확률은?
--> p(Rolex) = 250/2000 = 125/1000 = 0.125
q(Rolex) = 5/ 1000 = 0.005
r( Rolex ) = p(Rolex) / p(Rolex) + q(Rolex) = 0.125 / 0.125 + 0.005
단어가 더 많으면?
E1 = w1이 들어가는 경우
E2 = w2가 들어가는 경우
w1과 w2는 독립적이라고 가정하자.
이 두 개가 모두 들어가는 경우를 생각해보면
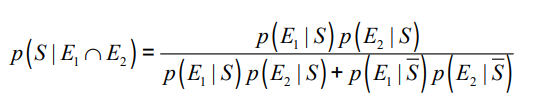
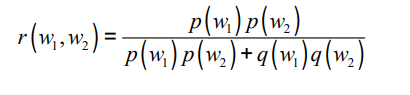
이와 같은 식이 나온다.
예제)
spam 메시지 총 2000개
아닌 거 총 1000개
p ( stock ) spam 에서 stock 이란 단어 400번 → 400 / 2000 = 0.2
q ( stock ) non spam에서 stock 이란 단어 60번 → 60 / 1000 = 0.06
p ( undervalued ) spam 에서 undervalued 이란 단어 200번 → 200 / 2000 = 0.1
q ( undervalued ) = non spam에서 undervalued 이란 단어 25번 → 25 / 1000 = 0.25
r ( stock, undervalued ) = p(stock) p(undervalued) / p(stock) p(undervalued) + q(stock) q(undervalued)
= ( 0.2 * 0.1 ) / ( 0.2 * 0.1 ) + ( 0.06 * 0.025 ) = 근 0.930
(참고)
https://www.youtube.com/watch?v=euH9C61ywEM
베이즈 정리
https://jesus-never-fail.tistory.com/19
위에 있는 내용 그대로 정리한 사람
나보다 잘함
+ PDF 똑같은데 그냥
(출처)
한동대학교 최희열 교수님 - 이산수학
'2학년 2학기 > 이산수학' 카테고리의 다른 글
| [ 이산 수학 ] 14. 관계 (0) | 2023.11.10 |
|---|---|
| [ 이산 수학 ] 13. 확률 분포 (0) | 2023.11.06 |
| [ 이산 수학 ] 11. 확률 (0) | 2023.10.26 |
| [ 이산 수학 ] 10. 경우의 수 (0) | 2023.10.13 |
| [ 이산 수학 ] 9. 재귀함수 / tree (0) | 2023.10.05 |




