오래 못 할 짓 하지 않기
[ 이산 수학 ] 13. 확률 분포 본문
기댓값
확률변수 X가 취하는 값 x1, x2, ... , xn에 대한 확률분포가 p1, p2, ... , pn일 때, 평균을 구하면
E(X) = x1p1 + x2p2 + ... + xn*pn


X를 주사위를 던졌을 때 나오는 숫자라고 해보자
X의 기댓값은?
[1부터 6까지 ] → (n) * ( n이 나올 확률 )

동전을 3번 튕겼을 때 나올 수 있는 경우에서, 확률변수 X를 Head 면이 나온 횟수라고 하자.
X의 기댓값은?
가능한 경우의 수
3개: HHH
2개 : HHT,HTH, THH
1개 : HTT,THT,TTH
0개 : TTT
이렇게 되어 있을 때,
3개일 때는 하나의 경우만 나오므로 1/8
1, 2개일 때는 3개의 경우이므로 3/8
0개일 때는 하나의 경우이므로 1/8
=> ( 3 * 1/8 ) + (2 * 3/8) + (1 * 3/8) + (0 * 1/8)
= 1.5

확률이 항상 p로 일정하고 시행횟수가 n이면 다음과 같은 식이 성립한다.

● k= 1~n일 때 , p(k) = C(n,k) p^k * q^(n-k)
● k * C(n,k) = C(n , k-1)
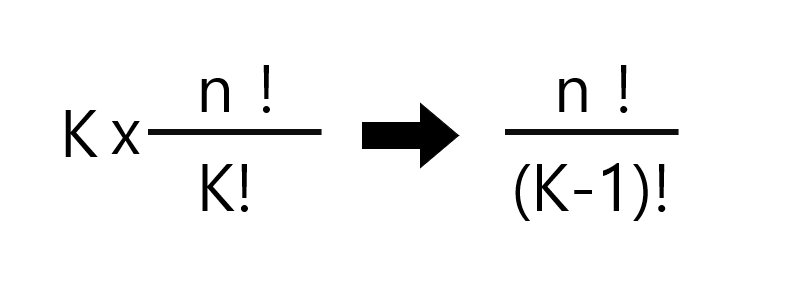
● C(n , k-1) = n C(n-1 , k-1)
n! = n * (n-1)!
이렇게 되면 n번째 확률은 계산하지 못하므로
np로 묶어서 시그마 밖으로 빼준다.
그러면 n번째 항은 세지 않으므로, 시그마의 범위를 바꿔준다.
k -1 의 범위가 1 ~ n 이므로, k-1를 하나의 문자로 치환한 j의 범위가 0~n-1 이 된다
● 다 더하면 p와 q를 합한 값들이 나올텐데 그건 어차피 1이므로 np만 구하면 된다.
따라서 E(X) = 시그마 kp (k는 1부터 n까지 , X=k)
= np
특징
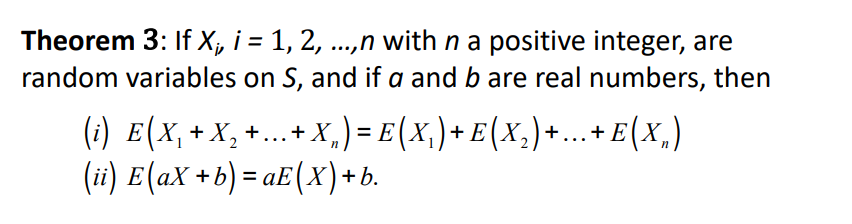
1) 여러 확률변수 합의 기댓값은, 각각의 확률 변수 기댓값을 합한 것과 같다.
2) E(aX + b) 의 기댓값은 E(X) * a + b와 같다.
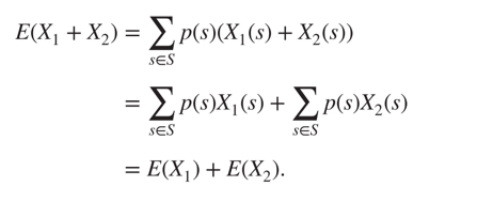
1) 특징으로 풀 수 있음 , 그걸 디테일하게 보여준 것
(+ E(x) = p(s)X(s) )
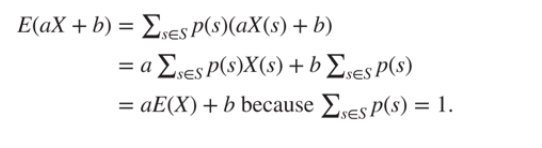
2) 특징으로 풀 수 있음 , 그걸 디테일하게 보여준 것
(+ E(x) = p(s)X(s) )
예제)

동전을 던져서 Tail 면이 나올 때까지 던진다고 했을 때, 기댓값은?
--> 가능한 경우의 수로는 T, HT, HHT, HHHT, HHHHT ... 형태로 있다.
p가 tail면이 나오는 확률이므로
p(T) = p p(X=1)
p(HT) = (1-p) p = p(X=2)
p(HHT) = (1-p)^2 p = p(X=3)
...
P(HHH...T) = (1-p)^(n-1) p = p(X=n)
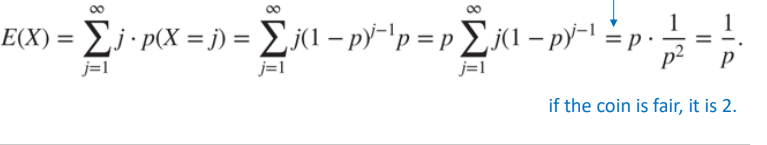


어떤 걸 성공할 때까지 시행을 한다면, 그에 대한 기댓값은 성공할 확률의 역수이다.
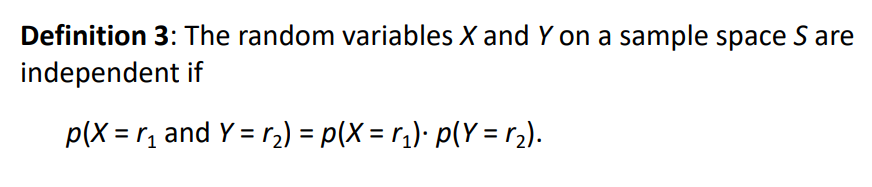
p( X=r1 and Y=r2 ) = p(X=r1) * p(Y=r2) 이 성립하면
X와 Y는 독립적이라고 할 수 있다.
p(1/6 * 1/6) = p(1/6) * p(1/6)

- X , Y: 주사위를 던져서 나온 2개의 수
- Z : X,Y의 합
(왼쪽) X가 1이 나오고 Z는 12일 확률=0
(오른쪽) X가 1이 나올 확률 = 1/6 * Z가 12일 확률 = 1/36
둘을 곱하면 0은 아니다.
독립이 아님!

천천히 이해해보기로
Variance
V(x) = 편차 제곱의 평균
= ( 값 - 평균 )^2 / n(개수)
= Sigma (s E S) (X(s) - E(X)) ^2 p(s)

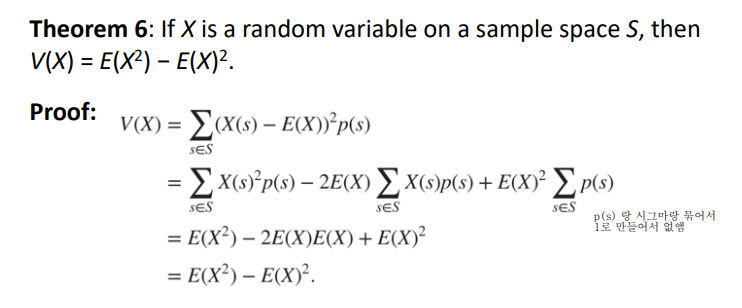
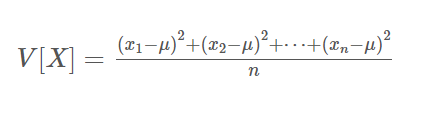
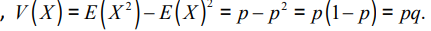
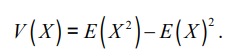
예제)

주사위를 굴렸을 때 나오는 숫자 X
X에 대한 분산은?
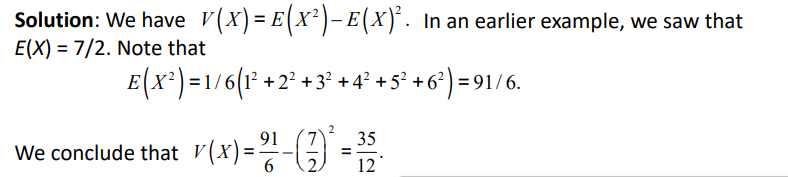
Bienaymé‘s Formula : X,Y가 독립이면, V(X+Y) = V(X)+V(Y)
Futhermore, V(X1+X2+X3...+Xn) = V(X1)+V(X2)+V(X3) + ... +V(Xn)
Proof
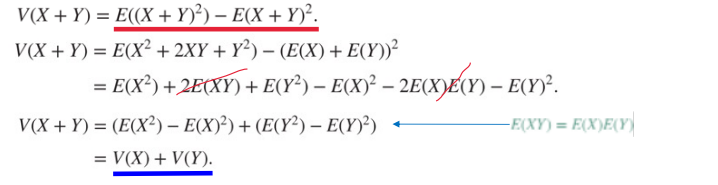

독립적인 확률의 일이 n번 수행되었을 때, p가 성공확률 / q가 실패확률
이 때 분산은?
V(X) = npq
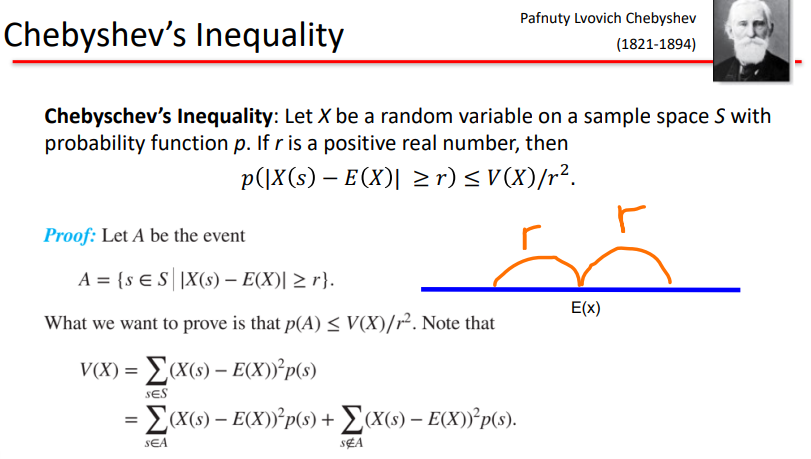
(참고)
분산 파트
https://hsm-edu.tistory.com/1459
확률변수의 독립
'2학년 2학기 > 이산수학' 카테고리의 다른 글
| [ 이산 수학 ] 15. 관계(2) (0) | 2023.11.13 |
|---|---|
| [ 이산 수학 ] 14. 관계 (0) | 2023.11.10 |
| [ 이산 수학 ] 12. 조건부 확률 2 (0) | 2023.10.30 |
| [ 이산 수학 ] 11. 확률 (0) | 2023.10.26 |
| [ 이산 수학 ] 10. 경우의 수 (0) | 2023.10.13 |




