오래 못 할 짓 하지 않기
[ 알고리즘 ] 1. Function 의 성능 분석 본문

함수 f(n)의 성능을 분석하는 방법으로는 다음과 같이 5개가 있다.
우리가 주로 볼 것은 Theta 와 Big - O 이다.
● Theta는 f(n)과 g(n)의 성능이 비슷비슷할 때를 의미하고
● Big-O는 f(n)의 성능이 g(n)의 성능보다 같거나 낮을 때를 의미한다.

n이 무한대일 때 [ f(n) / g(n) ] 의 값이 무한대가 아니라면
f(n) = O(g(n))이라고 할 수 있다.
( *예를 들어 f(n) = 2n^2 / g(n) = n^3 일 때 값은 0이다.)
O-notation은 주로 f(n)의 upper bound를 나타낸다.

이거를 이해해보려면
O(n^2) 일 때 여기에 속하는 집합 f(n)으로는
{ n^2 , 2n^2 -1 , 100n^2 , n , log n , }이 있다.
n^2 큰 제곱은 안 된다. ex) n^3 , n^4 는 안 됨.
Ω notation

Ω notation은 O notation과 반대라고 생각하면 된다.
f(n)의 아래 영역을 의미한다.
θ notation

Ω notation와 O natataion을 동시에 만족하는 걸 의미한다.
f(n) = g(n)가 완벽하게 일치함을 의미한다.
가능한 한 Ω notation / O natation / θ notation 세 개를 정확하게 표현해주는 게 좋다.
2n^2 은 O(n^2) , Ω(n^2) , θ(n^2) 셋 다 충족하지만
Ω notation와 O natataion을 동시에 만족하기 때문에
세타를 쓸 수 있으니 이걸 쓰는 게 바람직하다.
Little O notation
= 그냥 작으면 됨 , 근데 같으면 안 됨
f(n)=n, n^2은 o(n^3)에 들어간다.
little omega notation
= 그냥 크면 됨 , 근데 같으면 안 됨
시험에서 Time Complexity를 적으라고 했을 때
n^2 , n^3
이러는 사람들이 있는데, 이건 옳지 않음
O , w, omega , 세타 확실하게 해놔야함.
O( n^3 + n^2 ) 이거도 아님 그냥 O(n^3)만

요약하면 다음과 같다.
근데, 가능한 한 정확하게(Tight) 하는 게 원칙이다.
예를 들어 f(n) = n^2 + n 이라면
이는 θ ( n^2) , O(n^2) , o(n^3)도 가능하다.

문제에 대한 Lower bound 와 Worst case가 일치하다면
그 알고리즘은 Optimal하다고 한다.
optimal = 이게 제일 좋은 거다 X ,
언제든지 이 정도로는 빨리 풀 수 있다. O

출처: https://hoororyn.tistory.com/13

어떤 사람이 이 문제를 푸는데 " 최소 " n^2은 걸린다고 증명했다고 하자.
그렇다면 알고리즘1은 Optimal하다고 할 수 있다.
하지만 누군가 이 문제를 푸는데 최소 n이 걸린다고 할 때,
위 3개의 알고리즘은 아무것도 Optimal하지 않다
> 왜냐? 가장 빠른 게 n^2이었는데 더 빠른 n이 나왔으니까

데이터의 양이 충분히 많을 때 = n이 충분히 클 때
θ (n^2) 알고리즘은 θ (n^3)보다 항상 빠르다.
하지만, n0보다 데이터 양이 적을 때는 θ (n^3) 가 더 빠를 수도 있다.

뭐가 더 큰지 모르겠다 싶으면 n이 무한대로 간다고 해보면 된다.
분자와 분모를 미분해서 값을 구하면 된다~~
[ 돌발 퀴즈 ]
● 위 그림에서O( n^ (1/1000) ) 은 어디로 갈까?
O( log n ) 과 O(루트n)사이에 있을 것이다.
그럼 O( log n ) 과 O( n^ (1/1000) ) 중에 뭐가 더 클까?
▶
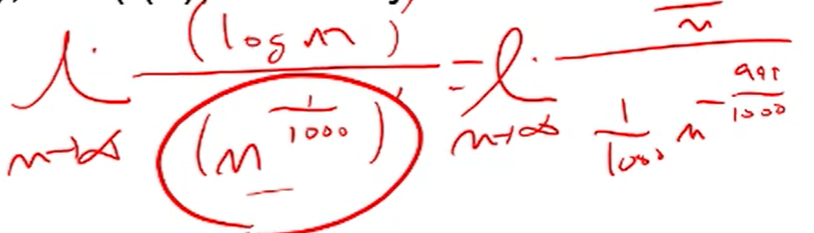

지수에 음수가 있고, 분모의 분모가 있어서 헷갈릴텐데 차근차근 계산해보면 이게 맞다.
===================▼ 정정
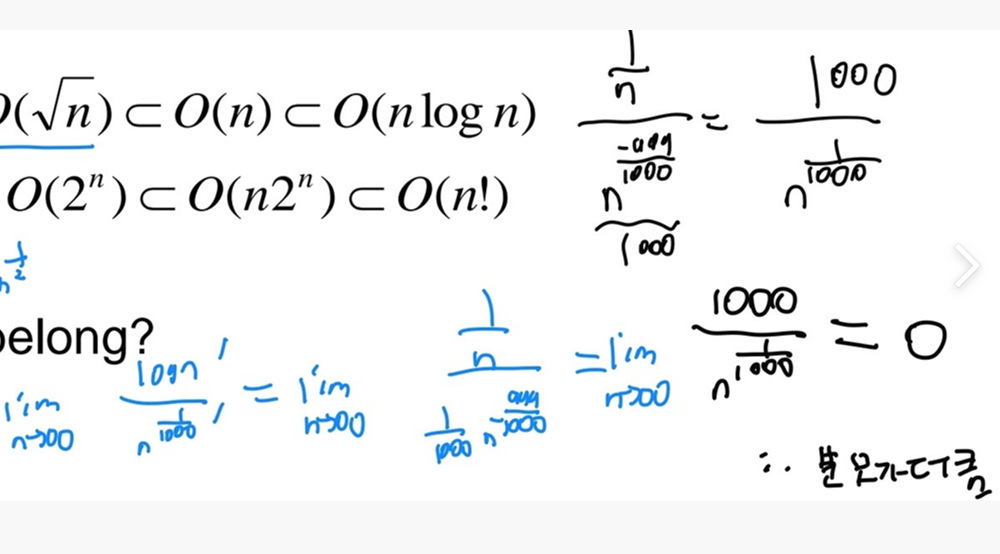
(출처)
한동대학교 용환기 교수님 - 알고리즘 ppt
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 4. Dynamic Programming (0) | 2024.03.24 |
|---|---|
| [ 알고리즘 ] 3-1 문제 풀이 (0) | 2024.03.23 |
| [ 알고리즘 ] 3. Divide and Conquer (1) | 2024.03.20 |
| [ 알고리즘 ] 2. Function 성능 관련 문제 (0) | 2024.03.16 |
| [ 알고리즘 ] 다이나믹 프로그래밍 (DP) (0) | 2024.02.07 |




