오래 못 할 짓 하지 않기
[ 알고리즘 ] 2. Function 성능 관련 문제 본문

f(n) =< c g(n)이라고 할 때
5n^2 = O(n^3) 라고 가정하면
n과 c가 어떻게 되어야 하는가?
현재 형태를 식에 맞춰보면
0 ≤ 5n^2 ≤ c * n^3 이렇다.
0 ≤ f(n) ≤ c * g(n)
c가 어떻게 되든 g(n)의 계수가 작아지지 않고
n이 어떤 상수가 되든 f(n)의 계수가 커지지 않으므로
답은 무수히 많다.
질문 : C도 고려를 해야하나? 상수는 떼고 그냥 차수만 생각하면 되는 거 아니었음?
2번

문제 풀기 전에 Notation 사이에 =가 있고
f(n) = g(n)이런 꼴이라면
→ f(n)은 g(n) 노테이션 종류에 속한다.
1) O - O(n^3)는 5n^2보다 크거나 같다.
2) X - 위에 설명했으니 패스
3) n^2 + cn = O(n^2) 맞음
4)
5) 같으면 안 됨
3번

2^(n+1) = 2* 2^n = 2^n으로 취급
...
i) 2^n = O(2^n)
→ 같아도 되니까 O
ii) 2^n = 오메가(2^n)
→ 같아도 되니까 O
iii) 2^n = 세타(2^n)
→ O랑 오메가에서 통과했으니 O
4번

lgn = log8 n 보다 3배 빨리 증가함
근데 차수는 셋 다 같으니 셋 다 참임
5번

Heap의 조건
1) Complete Binary Tree여야 한다. = 중간에 빈틈 X
2) Max , Min tree여야 한다.
1. 중간에 빈틈이라 Heap 아님
2. 55가 있을 자리가 아님

3. 가능
6번

1) 맞음.
2) 그걸 보장하지는 않음
ex) 3,1,2일 땐 가장 작은 게 1인데 마지막엔 2가 있음
7번
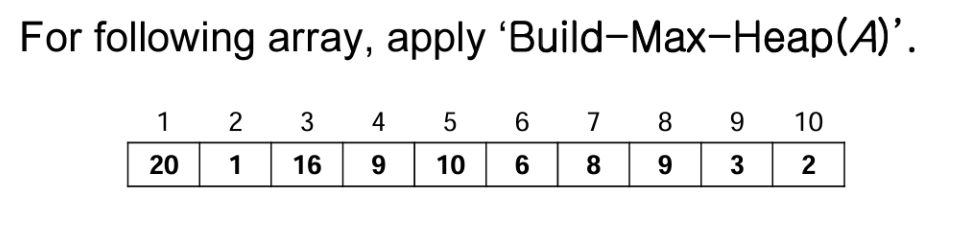

처음엔 이 모양이다.
이럴 때는 밑에서부터 삼각형으로 Heap을 만들어야 한다.
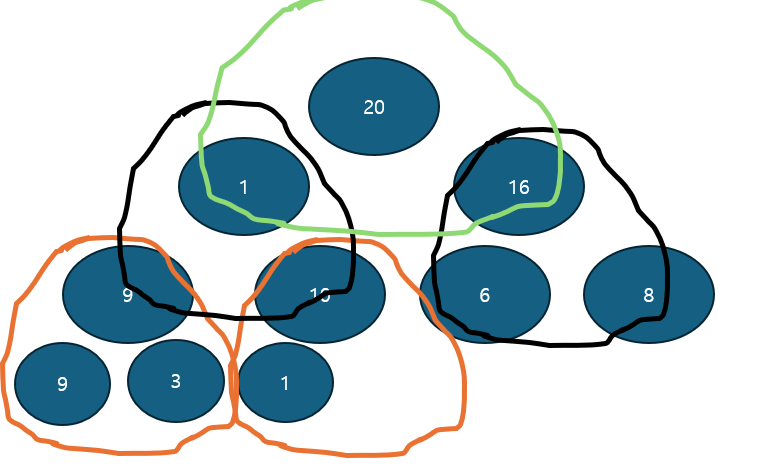
주황색 → 검은색 → 초록색
순서대로 Heap을 만들어간다. 그 결과는?

8번


(출처)
한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 4. Dynamic Programming (0) | 2024.03.24 |
|---|---|
| [ 알고리즘 ] 3-1 문제 풀이 (0) | 2024.03.23 |
| [ 알고리즘 ] 3. Divide and Conquer (1) | 2024.03.20 |
| [ 알고리즘 ] 1. Function 의 성능 분석 (0) | 2024.03.10 |
| [ 알고리즘 ] 다이나믹 프로그래밍 (DP) (0) | 2024.02.07 |





