오래 못 할 짓 하지 않기
[ 알고리즘 ] 3-1 문제 풀이 본문
문제 1
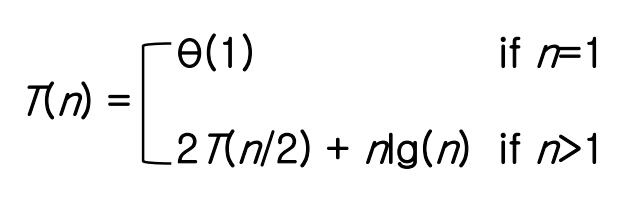
1. Recursion Tree 그리기
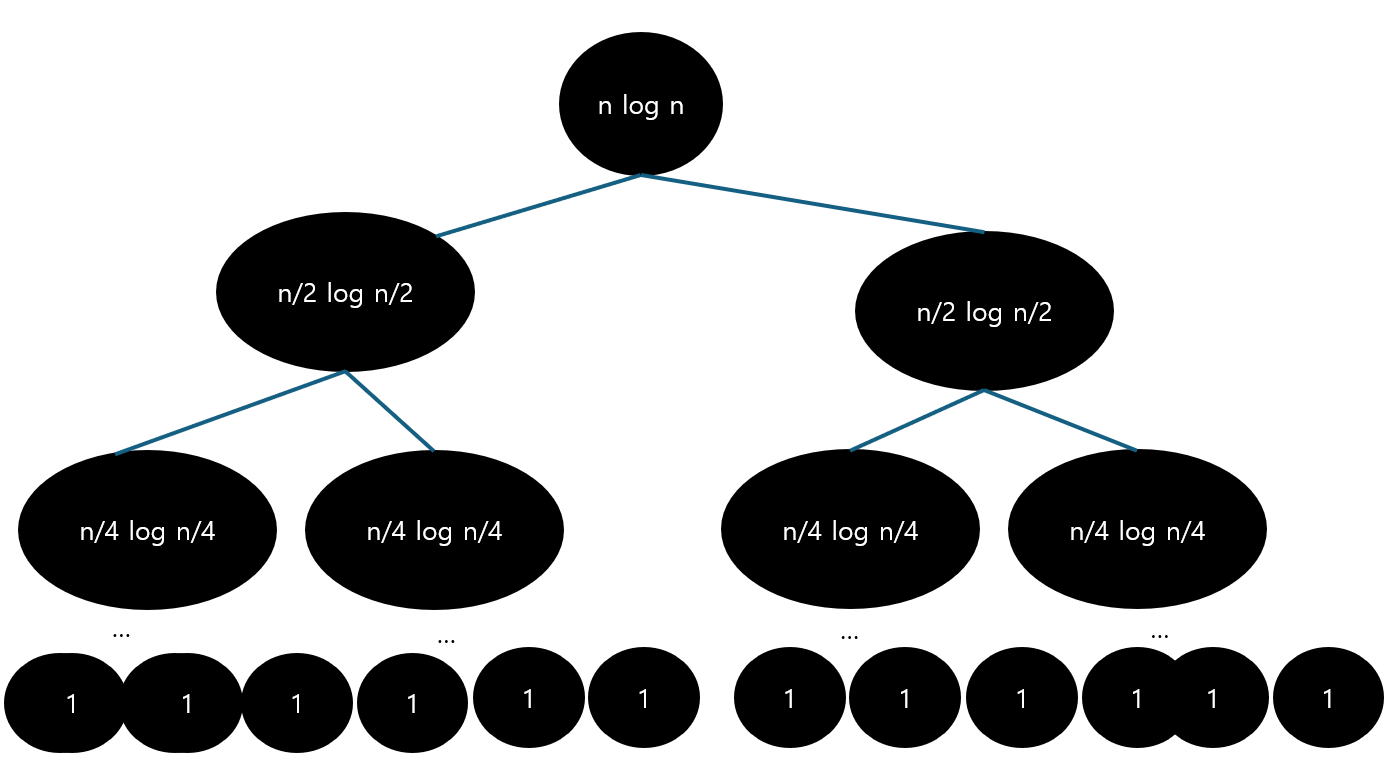
위와 같은 형태로 나온다.
● 특정 Level a에서의 node의 개수 = 2^a 개
● Tree 높이 = T(n)이 그 다음 단계에서 얼만큼 줄어드는지 보면 된다. = T(n/2)
= 이런 경우에 마지막 높이일 때 줄어들어 있는 정도는 [ n/2^마지막 높이 ] 일 것이다.
→ n / 2^h = 1
→ h = log2 n
● 각 레벨별 합
lv 0 : cn log (n) << 세타 n log(n) 이면, cn log(n)이라고 하는데, 식에는 세타가 없는데?
lv 1 : cn log (n/2)
lv 2 : cn log (n/4)
...
lv h : cn log (n/2^log2 n)
= cn * {(log n + log n +...) - log( 0+1+2+3+...)
분자 분모
... >log n +log n +log n +log n +... 이건 log n ^( 항의 개수 )
여기에서 항의 개수 = h = log 2 n
log n ^( log2 n )
= log n^2
= cn * { log n^2 - 1/2 log n * (log n+1) } << 굵게 해놓은 것들 끼리 계산하면 [ -1/2 log n^2 -1/2 log (n) ]
(0~n까지의 합 공식)
= cn * { 1/2 log n^2 + 1/2 log n }
= 계수들 빼고 계산하면 n* log n^2 + n* log n
= T(n) = 세타 n log^2 (n)
2. Master Theorom
a=2, b=2
log 2 2 =1
f(n) = n log(n)
case 1) O(n^(1-e)) =아님
case 2) 세타(n^1) = 아님
case 3) 오메가(n(1+e))
판단하려면 두 식을 나눠서 극한값으로 보내고, 그게 0보다 크고 무한대가 아니면 된다.
n log(n) / n ^(1+e)
= log(n) / n^e
이 때 뭐가 안 나눠지니까
둘 다 미분을 한다.
1/n / e n^(e-1) (계수로 있는 e는 무시)
나누기의 나누기 , n^-1 있으니 식을 정리해보면
= n^(1-e) / n
= 1/n^e
이다.
n이 무한대로 가면 값이 0이 된다.
이렇다면 분모로 갔던 n(log b^(a+e) 가 더 크다는 의미이다.
case 3에도 속하지 않으므로
어느 case에도 속하지 않는다.
문제 2

master theorem
a=4 , b=4 => n
f(n) = lg(n)
case1 ) lg(n) = O (n^1-e ) )
만약 e = 1/2보다 작으면 다 가능
case2 ) lg(n) = 세타 (n^1) x
case3 ) lg(n) = 오메가 (n^lg1+e) x
문제 3
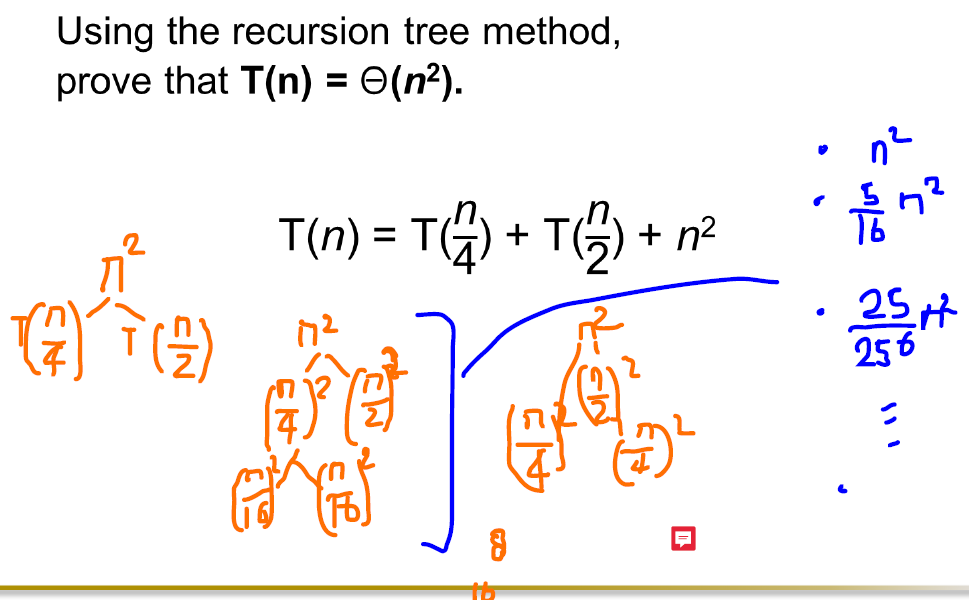
level by level total
:
T(n) =< n^2 ( 1 + 5/16 + (5/16)^2 + ... (5/16) ^k +...)
= < n^2 ( 1/ 1-(5/16) ) < 2 n^2
따라서 T(n) = O(n^2)
추가로 식을 보면 n^2에 두 개를 더하므로, n^2보다는 크다. 따라서
T(n) = 오메가 (n^2) 이다.
오메가와 O 둘 다 통과하므로, 세타 (n^2) 이다.
(출처)
한동대학교 용환기 교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 5. DP - MCM 알고리즘 (0) | 2024.03.31 |
|---|---|
| [ 알고리즘 ] 4. Dynamic Programming (0) | 2024.03.24 |
| [ 알고리즘 ] 3. Divide and Conquer (1) | 2024.03.20 |
| [ 알고리즘 ] 2. Function 성능 관련 문제 (0) | 2024.03.16 |
| [ 알고리즘 ] 1. Function 의 성능 분석 (0) | 2024.03.10 |





