오래 못 할 짓 하지 않기
[ 알고리즘 ] 3. Divide and Conquer 본문
● Recurrences
: 현재 주어진 함수를 더 작은 함수로 쪼개서 설명하는 방법
방법 1) Substitution Method
: 푸는 방법이라기보단 알고있는 게 맞다는 걸 증명하는 방법
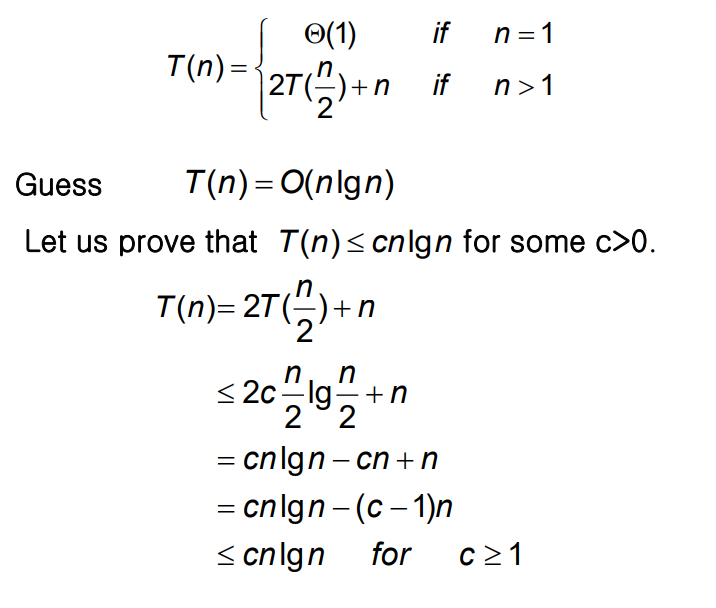
방법 2) Recursion - tree
: Recursion tree를 만든다.
- 각각의 node는 또 다른 작은 문제를 담고있다.
→ 각 Level의 cost를 합한다.
→ 모든 Level의 cost를 합한다.


이거 직접 손으로 풀어보기

T(1)은 constant한 값이다.
트리에 있는 Node의 합을 구하기 위해서는
Height를 알아야 한다.


각 레벨마다 Sum을 구했으니
그걸 다 더한다.
각 층을 내려갈 때마다 c뒤에 붙는 것의 분모가 1/4이 됨.
= 등비수열의 합


▼ 풀이
방법 3) Iteration (점화식)
:

두 번째 줄까지만 하면 이해 될거임
c + s(n-1)
= c + ( c + s(n-2) )
= c + c + ( c+ s(n-3) )
...

예제 1)

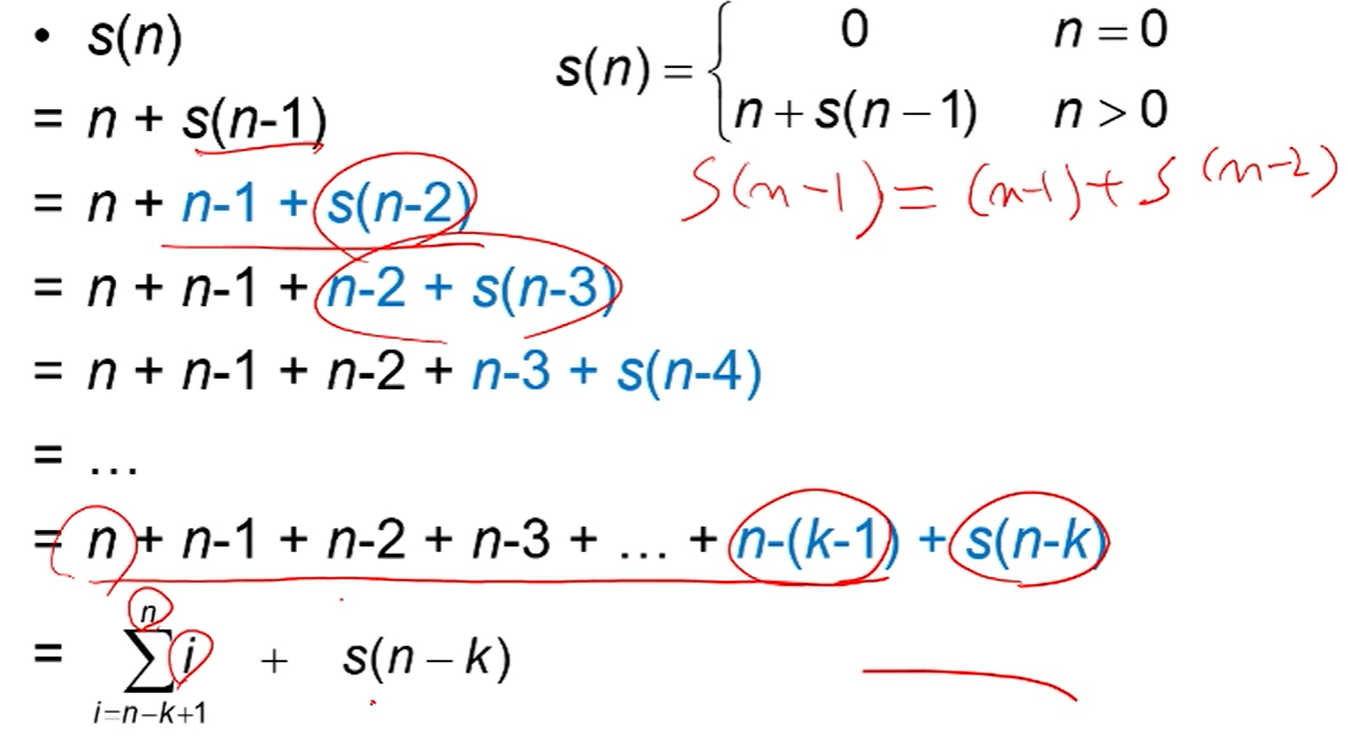

방법 4) Master Theroem

→ T(n) = a T(n/b) + f(n) 식일 때
f(n) 과 n log b^a 를 비교
1) f(n) 이 n^logb^(a-e) ▶ e가 0보다 큰 값을 넣었을 값과 같거나 더 작으면?
T(n) ,= Θ (n^log b^a) 이다.
2) f(n) 이 n^log b^a 와 같으면 ,
T(n) = Θ (n^log b^a lg n ) 이다.
3)

f(n) = n^2으로 바꿔보자
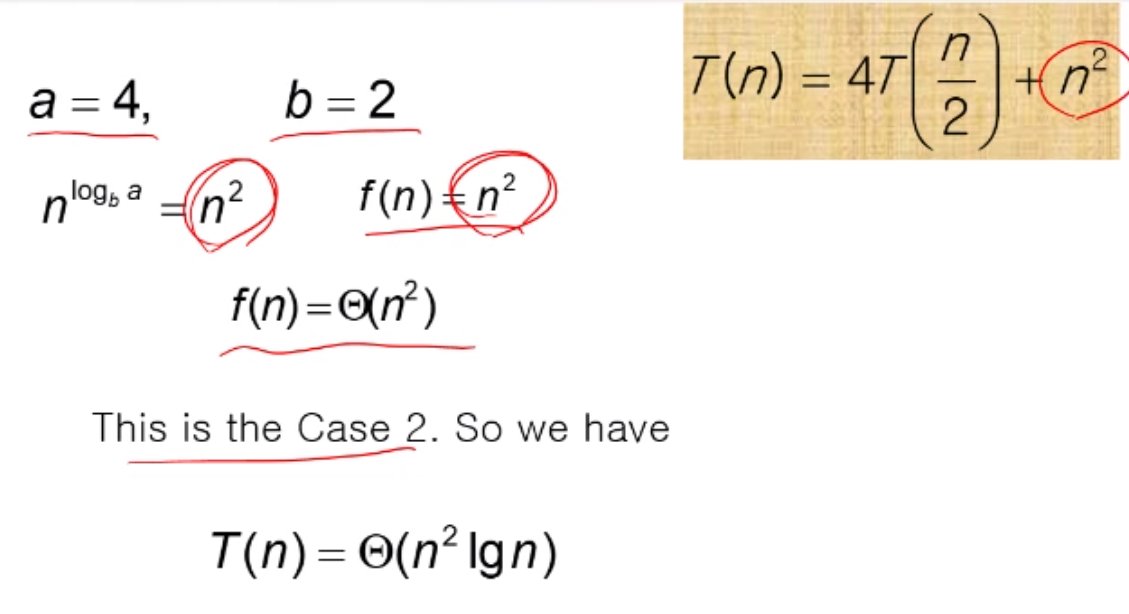
f(n) = n^3으로 바꿔보자

문제 풀기
1번
Iteration으로 풀기

각각의 for loop가 n으로 되어있고, 그 loop가 3겹으로 중첩되어 있기 때문에
Time complexity는 Θ (n^3) 이다.

▼ Divide and Conquer로 풀기
Time Complexity 구하기
1) Recursion Tree
n = 1일때, 4번째 줄만 수행하면 된다.
n> 1 일 때 , 하나의 일이 8개로 나뉘고, 그걸 모두 합한다.

8개로 나눠지는 건 ㅇㅋ
n*n인 행렬이 n/2 * n/2 로 바뀌기 때문에
한 변 기준으로 생각하면 될 것 같다.
( = n/4 이 아니다! )
Θ(n^2 ) = Divide하고 Combine하는데 걸리는 시간
컬럼을 n/2 * n/2로 나눴는데, 거기에 있는 것들을 다 세어야 하니까
n^2 / 4 이다.
계수 다 떼면 n^2이므로
Θ(n^2 )

식을 구했으니 더 세세하게 구해보자.

가장 마지막에 T(1)이 몇 개 있을까?
8^log n 개 있다.

(출처)
한동대학교 용환기교수님 - 알고리즘
'3학년 1학기 > 알고리즘 (Algorithm)' 카테고리의 다른 글
| [ 알고리즘 ] 4. Dynamic Programming (0) | 2024.03.24 |
|---|---|
| [ 알고리즘 ] 3-1 문제 풀이 (0) | 2024.03.23 |
| [ 알고리즘 ] 2. Function 성능 관련 문제 (0) | 2024.03.16 |
| [ 알고리즘 ] 1. Function 의 성능 분석 (0) | 2024.03.10 |
| [ 알고리즘 ] 다이나믹 프로그래밍 (DP) (0) | 2024.02.07 |





